
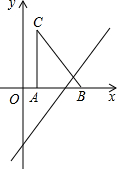 如圖,把Rt△ABC放在直角坐標系內,其中∠CAB=90°,BC=5,點A、B的坐標分別為(1,0)、(4,0).
如圖,把Rt△ABC放在直角坐標系內,其中∠CAB=90°,BC=5,點A、B的坐標分別為(1,0)、(4,0).分析 (1)根據勾股定理得出AC,再寫出點C坐標;
(2)根據題意,線段BC掃過的面積應為一平行四邊形的面積,其高是AC的長,底是點C平移的路程.求當點C落在直線y=2x-6上時的橫坐標即可.
解答  解:(1)∵點A、B的坐標分別為(1,0)、(4,0),
解:(1)∵點A、B的坐標分別為(1,0)、(4,0),
∴AB=3.
∵∠CAB=90°,BC=5,
∴AC=4.
∴點C的坐標是(1,4)
(2)如圖所示,∵AC=4,
∴A′C′=4.
∵點C′在直線y=2x-6上,
∴2x-6=4,解得 x=5.
即OA′=5.
∴CC′=5-1=4.
∴S?BCC′B′=4×4=16 (面積單位).
即線段BC掃過的面積為16面積單位.
故答案為(1,4),16.
點評 本題考查了一次函數圖象上點的坐標特征,平移的性質及一次函數的綜合應用,解決本題的關鍵是明確線段BC掃過的面積應為一平行四邊形的面積.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
 如圖所示,一棵8米高的筆直的杉樹在臺風中被刮斷,樹頂C落在離樹根B點4米處,科研人員要查看斷痕A處的情況,在離樹根B點1米的D處豎起一個梯子AD(點D、B、C在同一直線上),請問:這個梯子有多長?(結果請保留根號)
如圖所示,一棵8米高的筆直的杉樹在臺風中被刮斷,樹頂C落在離樹根B點4米處,科研人員要查看斷痕A處的情況,在離樹根B點1米的D處豎起一個梯子AD(點D、B、C在同一直線上),請問:這個梯子有多長?(結果請保留根號)查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | ab | B. | 3ab | C. | 3a2b2 | D. | 3a2b6 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{6}$ | C. | $\sqrt{24}÷\sqrt{3}=4$ | D. | $\sqrt{(-3)^{2}}=-3$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com