
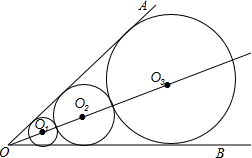
 如圖所示,已知∠AOB=60°,☉O1與∠AOB的兩邊都相切,沿OO1方向做☉O2與∠AOB的兩邊相切,且與☉O1外切,再作☉O3與∠AOB的兩邊相切,且與☉O2外切,…,如此作下去,☉On與∠AOB的兩邊相切,且與☉On-1外切,設☉On的半徑為rn,已知r1=1則r2016=32015.
如圖所示,已知∠AOB=60°,☉O1與∠AOB的兩邊都相切,沿OO1方向做☉O2與∠AOB的兩邊相切,且與☉O1外切,再作☉O3與∠AOB的兩邊相切,且與☉O2外切,…,如此作下去,☉On與∠AOB的兩邊相切,且與☉On-1外切,設☉On的半徑為rn,已知r1=1則r2016=32015. 分析 作輔助線,構建直角三角形,根據相似三角形的性質分別求半徑r2、r3、…、并找規律,得出結論.
解答 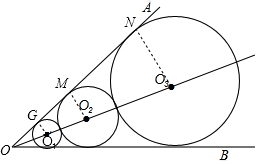 解:設⊙O1、⊙O2、⊙O3與邊OA的切點為G、M、N,
解:設⊙O1、⊙O2、⊙O3與邊OA的切點為G、M、N,
連接O1G、O2M、O3N,
則O1G⊥OA、O2M⊥OA、O3N⊥OA,
∴O1G∥O2M∥O3N,
∵⊙O1與∠AOB的兩邊都相切,∠AOB=60°,
∴∠AOO1=∠BOO1=30°,
∵OG=r1=1,
∴OO1=2,
∵O1G∥O2M,
∴△OO1G∽△OO2M,
∴$\frac{{O}_{1}G}{{O}_{2}M}$=$\frac{O{O}_{1}}{O{O}_{2}}$,
∴$\frac{1}{{r}_{2}}$=$\frac{2}{2+1+{r}_{2}}$,
∴r2=3,
同理得:$\frac{3}{{r}_{3}}$=$\frac{6}{6+3+{r}_{3}}$,
∴r3=9=32,
…
∴r2016=32015,
故答案為:32015.
點評 本題考查了切線長定理和切線的性質,本題可以看作是從圓外一點引圓的兩條切線,可以得它們的切線長相等,圓心和這一點的連線,平分兩條切線的夾角.根據這此結論與平行相似的判定結合,利用相似三角形的性質依次求圓的半徑即可.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
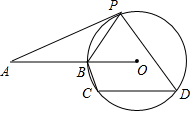 如圖,AP為☉O的切線,P為切點,若∠A=20°,C、D為圓周上兩點,且∠PDC=60°,則∠OBC等于( )
如圖,AP為☉O的切線,P為切點,若∠A=20°,C、D為圓周上兩點,且∠PDC=60°,則∠OBC等于( )| A. | 55° | B. | 65° | C. | 70° | D. | 75° |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | sinA=$\frac{1}{2}$ | B. | cosA=$\frac{1}{2}$ | C. | tanA=$\frac{1}{2}$ | D. | cotA=$\frac{1}{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com