
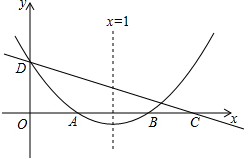
 如圖,直線y=kx+c與拋物線y=ax2+bx+c的圖象都經過y軸上的D點,拋物線與x軸交于A、B兩點,其對稱軸為直線x=1,且OA=OD.直線y=kx+c與x軸交于點C(點C在點B的右側).則下列命題中正確命題的是( )
如圖,直線y=kx+c與拋物線y=ax2+bx+c的圖象都經過y軸上的D點,拋物線與x軸交于A、B兩點,其對稱軸為直線x=1,且OA=OD.直線y=kx+c與x軸交于點C(點C在點B的右側).則下列命題中正確命題的是( )| A. | ①②③ | B. | ②③⑤ | C. | ②④⑤ | D. | ②③④⑤ |
分析 由拋物線的開口判斷a的符號;由對稱軸判斷b及b與2a的關系;由拋物線與y軸的交點判斷c的符號;由拋物線和直線圖象上點的坐標判斷有關代數式的符號.
解答 解:∵拋物線開口向上,
∴a>0.
∵拋物線對稱軸是x=1,
∴b<0且b=-2a.
∵拋物線與y軸交于正半軸,
∴c>0.
∴①abc>0錯誤;
∵b=-2a,
∴3a+b=3a-2a=a>0,
∴②3a+b>0正確;
∵b=-2a,
∴4a+2b+c=4a-4a+c=c>0,
∴④4a+2b+c<0錯誤;
∵直線y=kx+c經過一、二、四象限,
∴k<0.
∵OA=OD,
∴點A的坐標為(c,0).
直線y=kx+c當x=c時,y>0,
∴kc+c>0可得k>-1.
∴③-1<k<0正確;
∵直線y=kx+c與拋物線y=ax2+bx+c的圖象有兩個交點,
∴ax2+bx+c=kx+c,
得x1=0,x2=$\frac{k-b}{a}$.
由圖象知x2>1,
∴$\frac{k-b}{a}$>1
∴k>a+b,
∴⑤a+b<k正確,
即正確命題的是②③⑤.
故選B.
點評 本題考查的是二次函數圖象與系數的關系和一次函數的性質以及拋物線與直線的交點的求法,掌握一、二次函數的性質、靈活運用數形結合思想是解題的關鍵,解答時,要熟練運用拋物線的對稱性和拋物線上的點的坐標滿足拋物線的解析式.


 口算能手系列答案
口算能手系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
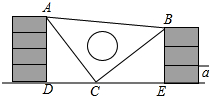 課間,小明拿著老師的等腰直角三角板的三角板玩,不小心掉到兩墻之間,如圖所示.
課間,小明拿著老師的等腰直角三角板的三角板玩,不小心掉到兩墻之間,如圖所示.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com