
分析 (1)直接根據銷售款=售價×套數即可得出結論;
(2)根據轉讓價格y(元/套)與轉讓數量x(套)之間的函數關系式為y=-$\frac{1}{10}$x+360(100≤x≤1200)得出總件數,再與售價相乘即可;
(3)把(1)(2)中的銷售款相加再減去成本即可.
解答 解:(1)∵甲經銷商庫存有1200套A品牌服裝,每套售價500元,轉讓x套給乙,
∴Q1=500×(1200-x)=-500x+600000(100≤x≤1200);
(2)∵轉讓價格y(元/套)與轉讓數量x(套)之間的函數關系式為y=-$\frac{1}{10}$x+360(100≤x≤1200),B品牌服裝,每套進價300元,
∴轉讓后可購買B服裝的套數=$\frac{x•(-\frac{1}{10}x+360)}{300}$元,
∴Q2=$\frac{x•(-\frac{1}{10}x+360)}{300}$×600=-$\frac{1}{5}$x2+720x(100≤x≤1200);
(3)∵由(1)、(2)知,Q1=-500x+600000,Q2=-$\frac{1}{5}$x2+720x,
∴W=Q1+Q2-400×1200=-500x+600000-$\frac{1}{5}$x2+720x-480000=-$\frac{1}{5}$(x-550)2+180500,
當x=550時,W有最大值,最大值為180450元.
點評 本題考查的是二次函數的應用,在商品經營活動中,經常會遇到求最大利潤,最大銷量等問題.解此類題的關鍵是通過題意,確定出二次函數的解析式,然后確定其最大值,實際問題中自變量x的取值要使實際問題有意義,因此在求二次函數的最值時,一定要注意自變量x的取值范圍.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
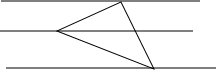 如圖,把一個等腰直角三角形放在間距是1的橫格紙上,三個頂點都在橫格上,則此三角形的斜邊長是( )
如圖,把一個等腰直角三角形放在間距是1的橫格紙上,三個頂點都在橫格上,則此三角形的斜邊長是( )| A. | 3 | B. | $\sqrt{10}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
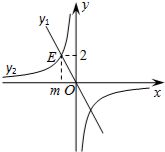 如圖,正比例函數y1=-2x與反比例函數y2相交于點E(m,2).
如圖,正比例函數y1=-2x與反比例函數y2相交于點E(m,2).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,一次函數y=-2x+8與反比例函數y=$\frac{k}{x}$(x>0)的圖象交于A(m,6),B(3,n)兩點.
如圖,一次函數y=-2x+8與反比例函數y=$\frac{k}{x}$(x>0)的圖象交于A(m,6),B(3,n)兩點.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 拋物線與x軸有兩個交點 | B. | 當x=1時,函數有最大值 | ||
| C. | 拋物線可由$y=-\frac{1}{2}{x^2}$經過平移得到 | D. | 當-1<x≤2時,函數y的整數值有3個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com