Question

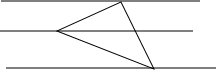
14．如圖，把一個等腰直角三角形放在間距是1的橫格紙上，三個頂點都在橫格上，則此三角形的斜邊長是（　　）

• A． 3
• B． $\sqrt{10}$
• C． 2$\sqrt{2}$
• D． 2$\sqrt{3}$

Answer 1

分析 作BD⊥a于D，CE⊥a于E則∠BDA=∠AEC=90°，證出∠ABD=∠CAE，由AAS證明△ABD≌△CAE，得出對應邊相等AE=BD=1，由勾股定理求出AC，再由勾股定理求出BC即可．

解答 解：如圖所示：作BD⊥a于D，CE⊥a于E，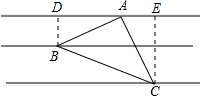
則∠BDA=∠AEC=90°，
∴∠ABD+∠BAD=90°，
∵∠BAC=90°，
∴∠CAE+∠BAD=90°，
∴∠ABD=∠CAE，
在△ABD和△CAE中，$\left\{\begin{array}{l}{∠BDA=∠AEC}{\;}\\{∠ABD=∠CAE}{\;}\\{AB=AC}{\;}\end{array}\right.$，
∴△ABD≌△CAE（AAS），
∴AE=BD=1，
∵CE=2，
∴由勾股定理得：AB=AC=，$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$，
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{10}$．
故選：B．

點評 本題考查了全等三角形的判定與性質、等腰直角三角形的性質、勾股定理；熟練掌握勾股定理，通過作輔助線證明三角形全等是解決問題的關鍵．