
如圖,直線y=﹣x+
 分別交x軸、y軸于A、B兩點,經過點A的直線m⊥x軸,直線l經過原點O交線段AB于點C,過點C作OC的垂線,與直線m相交于點P,現將直線l繞O點旋轉,使交點C在線段AB上由點B向點A方向運動.
分別交x軸、y軸于A、B兩點,經過點A的直線m⊥x軸,直線l經過原點O交線段AB于點C,過點C作OC的垂線,與直線m相交于點P,現將直線l繞O點旋轉,使交點C在線段AB上由點B向點A方向運動.
(1)填空:A( , )、B( , )
(2)直線DE過點C平行于x軸分別交y軸與直線m于D、E兩點,求證:△ODC≌△CEP;
(3)若點C的運動速度為每秒
 單位,運動時間是t秒,設點P的坐標為(
單位,運動時間是t秒,設點P的坐標為(
 ,a)
,a)
①試寫出a關于t的函數關系式和變量t的取值范圍;
②當t為何值時,△PAC為等腰三角形并求出點P的坐標.


【考點】一次函數綜合題.
【分析】(1)把x=0,y=0代入y=﹣x+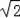
 解答即可;
解答即可;
(2)DE∥x軸,m⊥x軸,根據ASA證△ODC≌△CEP即可;
(3)①根據Rt△BDC中的勾股定理進行解答即可;
②根據等腰三角形和等腰直角三角形的性質進行解答.
【解答】解:(1)把x=0,y=0代入y=﹣x+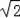
 ,可得:點A(
,可得:點A(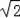
 ,0),B(0,
,0),B(0,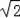
 );
);
故答案為:A(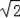
 ,0),B(0,
,0),B(0,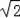
 );
);
(2)∵DE∥x軸,m⊥x軸,
∴m⊥DE,DE⊥y軸,
∴∠ODE=∠CEP=90°,
∵OC⊥CP,
∴∠OCP=90°,
∴∠DCO+∠ECP=180°﹣∠OCP=90°,
∴∠DCO+∠DOC=90°,
∴∠ECP=∠DOC,
∵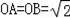
 ,
,
∴∠ABO=∠BAO,
∵DE∥x軸,
∴∠BCD=∠BAO,
∴∠ABO=∠BCD,
∴BD=CD,AE∥y軸,由平移性質得:OA=DE,
∴OB=DE,OB﹣BD=DE﹣CD,
∴OD=CE,
在△ODC與△CEP中,
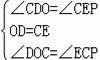
 ,
,
∴△ODC≌△CEP(ASA);
(3)①∵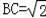
 t,BD=CD,
t,BD=CD,
在Rt△BDC中,BD2+CD2=BC2
∴BD=CD=t,OA=OB=
 ,DO=BO﹣BD=
,DO=BO﹣BD=
 ﹣t,EA=DO=
﹣t,EA=DO=
 ﹣t,
﹣t,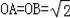
 ﹣t,EP=CD=t,AP=EA﹣EP=
﹣t,EP=CD=t,AP=EA﹣EP=
 ﹣2t,
﹣2t,
在Rt△AOB中,AO2+BO2=AB2
∴OA=2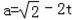
 (0≤t≤2),
(0≤t≤2),
②當t=0時,△PAC是等腰直角三角形

∴即點坐標是:P(
 ,
,
 ),PA=AC,則
),PA=AC,則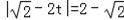
 t
t
解得t=1或t=﹣1(舍去)
∴當t=1時,△PAC是等腰三角形
即點坐標是:P(
 ,
,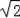
 ﹣2),
﹣2),
∴當t=0或1時,△PAC為等腰三角形,
點P的坐標為:P(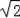
 ,
,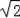
 )或P(
)或P(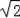
 ,
,
 ﹣2).
﹣2).
【點評】主要考查了函數和幾何圖形的綜合運用.解題的關鍵是會靈活的運用函數的性質和點的意義表示出相應的線段的長度,再結合三角形全等和等腰三角形的性質求解.試題中貫穿了方程思想和數形結合的思想,請注意體會.


科目:初中數學 來源: 題型:
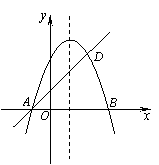
如圖,拋物線y=-x2+bx+c與x軸交于A、B兩點,且B點的坐標為(3,0),經過A點的直線交拋物線于點D (2, 3).
(1)求拋物線的解析式和直線AD的解析式;
(2)過x軸上的點E (a,0) 作直線EF∥AD,交拋物線于點F,是否存在實數a,使得以A、D、E、F為頂點的四邊形是平行四邊形?如果存在,求出滿足條件的a;如果不存在,請說明理由.
 |
查看答案和解析>>
科目:初中數學 來源: 題型:
下列調查中,適宜采用普查方式的是………………………………………………( )
A.了解一批圓珠筆的使用壽命 B.了解全國九年級學生身高的現狀
C.考察人們保護海 洋的意識 D.檢查一枚用于發射衛星的運載火箭的各零部件
洋的意識 D.檢查一枚用于發射衛星的運載火箭的各零部件
查看答案和解析>>
科目:初中數學 來源: 題型:
在括號內填寫理由.
如圖,已知∠B+∠BCD=180°,∠B=∠D.求證:∠E=∠DFE.
證明:∵∠B+∠BCD=180°( ),
∴AB∥CD ( )
∴∠B=∠DCE( )
又∵∠B=∠D( ),
∴∠DCE=∠D ( )
∴AD∥BE( )
∴∠E=∠DFE( )


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com