中考利劍中考試卷匯編系列答案
教育世家狀元卷系列答案
黃岡課堂作業本系列答案科目：初中數學 來源： 題型：
如圖，已知拋物線y=ax2+bx+c（a≠0）的頂點坐標為Q(-2，-1)，且與y軸交于點C(0，3)，與x軸交于A，B兩點（點A在點B的左側），點P是該拋物線上一動點，從點C沿拋物線向點A運動（點P與A不重合），過點P作PD∥y軸，交直線AC于點D．
（1）求該拋物線的函數關系式．
（2）當△ADP是直角三角形時，求點P的坐標．
（3）在問題（2）的結論下，若點E在x軸上，點F在拋物線上，問是否存在以A，P，E，F為頂點的平行四邊形？若存在，請直接寫出點F的坐標；若不存在，請簡單說明理由．
 |
查看答案和解析>>
科目：初中數學 來源： 題型：
設a,b是任意兩個不等實數，我們規定：滿足不等式a≤x≤b的實數x的所有取值的全體叫做閉區間，表示為{a,b},對于一個函數，如果它的自變量x與函數值y滿足：當m≤x≤n時，有m≤y≤n,我們就稱此函數是閉區間{m,n}上的“閉函數”.
（1）反比列函數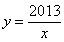
是閉區間{1,2013}上的“閉函數”嗎？請判斷并說明理由；
（2）若一次函數y=kx+b(k≠0)是閉區間{m,n}上的“閉函數”，求此函數的解析式：
查看答案和解析>>
科目：初中數學 來源： 題型：
19.如圖，⊙O中，弦AB、CD相交于AB的中點E，連接AD并延長至點F，使DF=AD，
連接BC、BF．
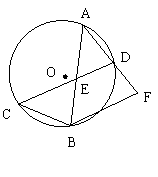（1）求證：△CBE∽△AFB；
（2）當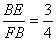
時，求
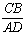的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
一個立方體展開后各面上分別標有數字1，2，3，4， 6，8，其表面展開圖如圖所示，拋擲這個立方體，則朝上一面的數字恰好等于朝下一面數字的2倍的概率是（ ）
A、
B、
C、
D、
查看答案和解析>>
科目：初中數學 來源： 題型：
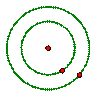
如圖，在以O為圓心的兩個同心圓中，大圓的直徑AB交小圓于C、D兩點，AC＝CD＝DB，分別以C、D為圓心，以CD為半徑作圓．若AB＝6cm，則圖中陰影部分的面積為 cm2．
查看答案和解析>>
科目：初中數學 來源： 題型：
如圖，有2個同心圓，半徑分別為R和r（單位：厘米）,且R>r>1，記兩圓之間的圓環面積為P；若把R和r都增加1厘米，記兩圓之間的圓環面積為Q，則：…………………………………………………( )
A： 0<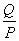
<1 B： 1<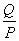<2 C： 2<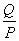<3 D： 3<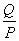<4
查看答案和解析>>
科目：初中數學 來源： 題型：
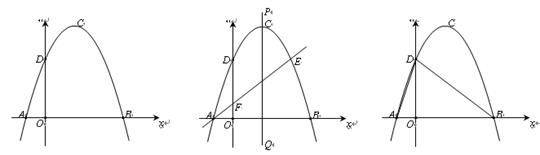
如圖1，拋物線y=ax2＋bx＋c(a≠0)的頂點為（1,4），交x軸于A、B兩點，交y軸于點D，其中B點的坐標為（3,0）.
（1）求拋物線的解析式.
（2）如圖2，過點A的直線與拋物線交于點E，交y軸于點F，其中E點的橫坐標為2，直線PQ為拋物線的對稱軸.①說明點D與點E關于直線PQ對稱.
②若點G為PQ上一動點，則x軸上是否存在一點H，使D、G、F、H四點圍成的四邊形周長最小？若存在，求出這個最小值及G、H的坐標；若不存在，請說明理由.
（3）如圖3，拋物線上是否存在一點T，過點T作x的垂線，垂足為M，過點M作直線MN∥BD，交線段AD于點N，連接MD，使△DNM∽△BMD，若存在，求出點T的坐標；若不存在，說明理由.
 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
的解是非負數，則m的取值范圍是 ．