Question

2．已知拋物線y=x²+x-2
（1）求拋物線與x軸的交點(diǎn)坐標(biāo)；
（2）將拋物線y=x²+x-2沿y軸向上平移，平移后與直線y=x+2的一個(gè)交點(diǎn)為點(diǎn)P，與y軸相交于點(diǎn)Q，當(dāng)PQ∥x軸時(shí)，求拋物線平移了幾個(gè)單位；
（3）將拋物線y=x²+x-2在x軸下方的部分沿x軸翻折到x軸上方，圖象的起步部分保持不變，翻折后的圖象與原圖象在x軸上方的部分組成一個(gè)“W”形狀的新圖象，若直線y=$\frac{1}{2}$x+b與該新圖象恰好有三個(gè)公共點(diǎn)，求b的值．

Answer 1

分析 （1）令y=0，得到關(guān)于x的方程，解方程即可求得；
（2）設(shè)平移后的拋物線為y=x²+x-2+n，求得與y的交點(diǎn)坐標(biāo)，根據(jù)題意，把交點(diǎn)縱坐標(biāo)代入y=x+2求得P的交點(diǎn)坐標(biāo)，把P的交點(diǎn)坐標(biāo)代入拋物線的解析式即可求得n的值．
（3）有圖象可得當(dāng)直線y=$\frac{1}{2}$x+b過點(diǎn)A時(shí)，直線y=$\frac{1}{2}$x+b與該新圖象恰好有三個(gè)公共點(diǎn)，易得對(duì)應(yīng)的b的值為1；當(dāng)直線y=$\frac{1}{2}$x+b與拋物線y=-（x+$\frac{1}{2}$）²+$\frac{9}{4}$（-2≤x≤1）相切時(shí)，直線y=$\frac{1}{2}$x+b與該新圖象恰好有三個(gè)公共點(diǎn)，即=-（x+$\frac{1}{2}$）²+$\frac{9}{4}$=$\frac{1}{2}$x+b有相等的實(shí)數(shù)解，利用根的判別式的意義可求出此時(shí)b的值．

解答 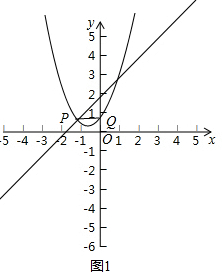解：（1）令y=0，則x²+x-2=0，解得x₁=-2，x₂=1，
∴拋物線與x軸的交點(diǎn)坐標(biāo)為（-2，0），（1，0）；
（2）設(shè)拋物線向上平移了n個(gè)單位，則平移后的拋物線為y=x²+x-2+n，
如圖1，∵拋物線y=x²+x-2+n與y軸的交點(diǎn)為（0，n-2），
∴P的縱坐標(biāo)為n-2，代入y=x+2得，x=n-4，
∴P（n-4，n-2），
∴拋物線y=x²+x-2+n的對(duì)稱軸為x=$\frac{n-4}{2}$=$\frac{1}{2}$n-2，
由拋物線y=x²+x-2+n可知對(duì)稱軸為x=-$\frac{1}{2}$，
∴$\frac{1}{2}$n-2=-$\frac{1}{2}$，解得n=3，
∴當(dāng)PQ∥x軸時(shí)，求拋物線平移了3個(gè)單位；
（3）∵y=x²+x-2=（x+$\frac{1}{2}$）²-$\frac{9}{4}$，
∴拋物線y=x²+x-2的頂點(diǎn)坐標(biāo)為（-$\frac{1}{2}$，-$\frac{9}{4}$），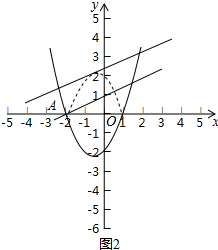
∴拋物線y=x²+x-2圖象x軸下方的部分沿x軸翻折到x軸上方，則翻折部分的拋物線解析式為y=-（x+$\frac{1}{2}$）²+$\frac{9}{4}$（-2≤x≤1），如圖2，
把直線y=$\frac{1}{2}$x向上平移，當(dāng)平移后的直線y=$\frac{1}{2}$x+b過點(diǎn)A時(shí)，直線y=$\frac{1}{2}$x+b與該新圖象恰好有三個(gè)公共點(diǎn)，所以$\frac{1}{2}$×（-2）+b=0，解得b=1；
當(dāng)直線y=$\frac{1}{2}$x+b與拋物線y=-（x+$\frac{1}{2}$）²+$\frac{9}{4}$（-2≤x≤1）相切時(shí)，直線y=$\frac{1}{2}$x+b與該新圖象恰好有三個(gè)公共點(diǎn)，即-（x+$\frac{1}{2}$）²+$\frac{9}{4}$=$\frac{1}{2}$x+b有相等的實(shí)數(shù)解，整理得x²+$\frac{3}{2}$x+b-2=0，△=（$\frac{3}{2}$）²-4（b-2）=0，解得b=$\frac{41}{16}$，
所以b的值為1或$\frac{41}{16}$．

點(diǎn)評(píng) 本題考查了二次函數(shù)與幾何變換：由于拋物線平移后的形狀不變，故a不變，所以求平移后的拋物線解析式通常可利用兩種方法：一是求出原拋物線上任意兩點(diǎn)平移后的坐標(biāo)，利用待定系數(shù)法求出解析式；二是只考慮平移后的頂點(diǎn)坐標(biāo)，即可求出解析式．