
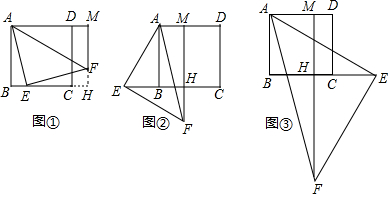
分析 (1)作輔助線,構建全等三角形,證明四邊形ABHM為矩形,則AM=BH,證明△ABE≌△EHF,AB=EH,根據線段的和得出結論;
(2)如圖②,AB=BE+AM,證明△AEB≌△EFH和四邊形ABHM為矩形,則AM=BH,所以AB=EH=BE+BH=BE+AM;
(3)如圖③,根據△AEF是等腰直角三角形,得∠AFE=45°,從而求得∠HFE=45°-15°=30°,同理得△ABE≌△EHF,則∠AEB=∠HFE=30°,由四邊形ABHM是矩形,得AM=BH=$\sqrt{3}$-1.
解答  證明:(1)延長MF,交BC延長線于H,
證明:(1)延長MF,交BC延長線于H,
∵四邊形ABCD為正方形,
∴∠BAM=∠B=90°,
∵FM⊥AD,
∴∠AMF=90°,
∴四邊形ABHM為矩形,
∴AM=BH,
∵△AEF是等腰直角三角形,
∴AE=EF,∠AEF=90°,
∴∠AEB+∠FEH=90°,
∵∠B=90°,
∴∠AEB+∠BAE=90°,
∴∠FEH=∠BAE,
∵∠B=∠EHF=90°,
∴△ABE≌△EHF,
∴AB=EH,
∴AM=BH=BE+EH=BE+AB;
(2)AB=BE+AM,理由是:
如圖②,∵△AEF是等腰直角三角形,
∴AE=EF,∠AEF=90°,
∴∠AEB+∠FEH=90°,
∵∠ABE=90°,
∴∠AEB+∠EAB=90°,
∴∠FEH=∠EAB,
∵∠ABE=∠EHF=90°,
∴△AEB≌△EFH,
∴AB=EH,
∵∠MAB=∠ABH=∠BHM=90°,
∴四邊形ABHM為矩形,
∴AM=BH,
∴AB=EH=BE+BH=BE+AM;
(3)如圖③,∵△AEF是等腰直角三角形,
∴∠AFE=45°,
∵∠AFM=15°,
∴∠HFE=45°-15°=30°,
同理得:△ABE≌△EHF,
∴∠AEB=∠HFE=30°,EH=AB,
Rt△ABE中,∴AE=2,AB=1,
∴BC=EH=AB=1,
∴BH=EC=$\sqrt{3}$-1,
同理得:四邊形ABHM是矩形,
∴AM=BH=$\sqrt{3}$-1.
故答案為:$\sqrt{3}$-1.
點評 本題是四邊形的綜合題,考查了三角形全等的性質和判定、矩形、等腰直角三角形的性質和判定、直角三角形30°角的性質、正方形的性質,本題的三個問題中證明△ABE≌△EHF是關鍵,在證明線段的和時,利用三角形全等中線段相等作等量代換及線段的和的關系得出結論.


 亮點激活精編提優100分大試卷系列答案
亮點激活精編提優100分大試卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 實數a,b在數軸上的位置如圖,化簡$\sqrt{(a-b)^{2}}$-$\frac{a(a+b)}{|a+b|}$的結果為( )
實數a,b在數軸上的位置如圖,化簡$\sqrt{(a-b)^{2}}$-$\frac{a(a+b)}{|a+b|}$的結果為( )| A. | b | B. | -b | C. | -2a+b | D. | 2a-b |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
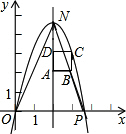 如圖,在直角坐標系中,點P的坐標是(n,0)(n>0),拋物線y=-x2+bx+c經過原點O和點P,已知正方形ABCD的三個頂點為A(2,2),B(3,2),D(2,3).
如圖,在直角坐標系中,點P的坐標是(n,0)(n>0),拋物線y=-x2+bx+c經過原點O和點P,已知正方形ABCD的三個頂點為A(2,2),B(3,2),D(2,3).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com