Question

6．如圖，已知平行四邊形ABCD中，AB=2$\sqrt{5}$，AD=6，cot∠ABC=$\frac{1}{2}$，將邊AB繞點A旋轉(zhuǎn)，使得點B落在平行四邊形ABCD的邊上，其對應點為B′（點B′不與點B重合），那么sin∠CAB′=$\frac{\sqrt{10}}{10}$或$\frac{\sqrt{2}}{2}$．

Answer 1

分析 過A作AH⊥BC，連接AC，求得∠ACB的度數(shù)，然后分成B′在BC上和在AD上兩種情況進行討論．當點B′落在BC上時，過B′作BM⊥AC，求得B′M的長，利用三角函數(shù)定義求得；當B′落在AD上時，∠CAB′=∠ACB，據(jù)此即可直接求解．

解答 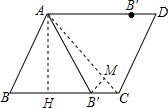解：過A作AH⊥BC，連接AC．
cotB=$\frac{BH}{AH}$=$\frac{1}{2}$，則2BH=AH．
∵BH²+AH²=AB²，
∴BH=2，AH=4，
∴HC=BC-BH=6-2=4，
∴AH=HC=4，
∴∠ACB=45°，
①當點B′落在BC上時，
∵直角△ABH和直角△AB′H中，
$\left\{\begin{array}{l}{AB=AB′}\\{AH=AH}\end{array}\right.$，
∴直角△ABH≌直角△AB′H．
∴BH=B′H=2，
∴B′C=2，
∴AC=$\sqrt{A{H}^{2}+H{C}^{2}}$=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$．
過B′作BM⊥AC，
∵∠ACB=45°，
∴△B′MC是等腰直角三角形，
∴B′M=CM=$\sqrt{2}$，
∴sin∠CAB′=$\frac{B′M}{AB′}$=$\frac{\sqrt{2}}{2\sqrt{5}}$=$\frac{\sqrt{10}}{10}$；
②當B′落在AD上時，∠CAB′=∠ACB=45°，
則sin∠CAB′=sin45°=$\frac{\sqrt{2}}{2}$．
總之，sin∠CAB′的值是$\frac{\sqrt{10}}{10}$或$\frac{\sqrt{2}}{2}$．
故答案是：$\frac{\sqrt{10}}{10}$或$\frac{\sqrt{2}}{2}$．

點評 本題考查了旋轉(zhuǎn)的性質(zhì)以及三角函數(shù)的定義，正確分成兩種情況進行討論是解決本題的關(guān)鍵．