
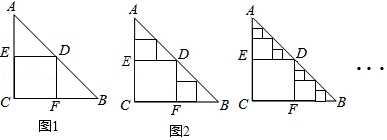
分析 根據題意,可求得S△AED+S△DBF=S正方形ECFD=S1=1,同理可得規律:Sn即是第n次剪取后剩余三角形面積和,根據此規律求解即可答案.
解答 解:∵四邊形ECFD是正方形,
∴DE=EC=CF=DF,∠AED=∠DFB=90°,
∵△ABC是等腰直角三角形,
∴∠A=∠B=45°,
∴AE=DE=EC=DF=BF=EC=CF,
∵AC=BC=2,
∴DE=DF=1,
∴S△AED+S△DBF=S正方形ECFD=S1=1;
同理:S2即是第二次剪取后剩余三角形面積和,
Sn即是第n次剪取后剩余三角形面積和,
∴第一次剪取后剩余三角形面積和為:2-S1=1=S1,
第二次剪取后剩余三角形面積和為:S1-S2=1-$\frac{1}{2}$=$\frac{1}{2}$=S2,
第三次剪取后剩余三角形面積和為:S2-S3=$\frac{1}{2}$-$\frac{1}{4}$=$\frac{1}{4}$=S3,
…
第n次剪取后剩余三角形面積和為:Sn-1-Sn=Sn=$\frac{1}{{2}^{n-1}}$,
故第64次剪取后,余下的所有小三角形的面積之和是:$\frac{1}{{2}^{63}}$.
故答案為:$\frac{1}{{2}^{63}}$.
點評 此題考查了正方形與等腰直角三角形的性質.此題難度較大,屬于規律性題目,找到規律:Sn即是第n次剪取后剩余三角形面積和是解此題的關鍵.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:選擇題
| A. | 三條高的交點 | B. | 三條角平分線的交點 | ||
| C. | 三條邊的垂直平分線的交點 | D. | 三條中線的交點 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
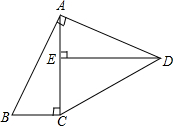 如圖,在四邊形ABCD中,∠BAD=∠ACB=∠AED=90°,AB=AD.
如圖,在四邊形ABCD中,∠BAD=∠ACB=∠AED=90°,AB=AD.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2個 | B. | 3個 | C. | 4個 | D. | 5個 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,兩幢大樓AB,CD之間的水平距離(BD)為20米,為測得兩幢大樓的高度,小王同學站在大樓AB的頂端A處測得大樓CD頂端C的仰角為60°,測得大樓CD的底部D的俯角為45°,試求大樓AB和CD的高度.(精確到1米)
如圖,兩幢大樓AB,CD之間的水平距離(BD)為20米,為測得兩幢大樓的高度,小王同學站在大樓AB的頂端A處測得大樓CD頂端C的仰角為60°,測得大樓CD的底部D的俯角為45°,試求大樓AB和CD的高度.(精確到1米)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com