
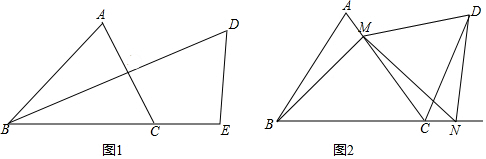
分析 (1)連接CD,構造含30°角的直角三角形DCE,根據BC=DC進行計算即可;
(2)過點N作NG⊥CD于G,作NH⊥AC于H,得到∠H=∠DGN=90°,先判定Rt△MNH≌Rt△DNG(HL),得到∠CMQ=∠NDQ,進而得出∠2=∠5=60°,最后結合NM=ND,判定△DMN為等邊三角形即可;
(3)需要分兩種情況進行討論:當點M在線段AC上時,連接AD,BD;當點M在CA延長線上時,連接AD,分別根據等高三角形的面積之比等于底邊之比進行計算即可.
解答 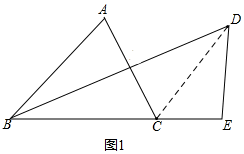 解:(1)如圖1,連接CD,
解:(1)如圖1,連接CD,
∵△ABC是等邊三角形,點D和點B關于直線AC軸對稱,
∴BC=DC,∠ACB=∠ACD=60°,
∴∠DCE=60°,
∵DE⊥CE,CE=5,
∴∠CDE=30°,
∴CD=2CE=10,
∴BC=10;
(2)如圖2,過點N作NG⊥CD于G,作NH⊥AC于H,則∠H=∠DGN=90°,
∵△ABC是等邊三角形,點D和點B關于直線AC軸對稱,
∴∠1=∠2=60°,
∴∠3=60°=∠4,即NC平分∠GCH,
∴NG=NH,
∵線段DM的垂直平分線交直線BC于點N,
∴NM=ND,
在Rt△MNH和Rt△DNG中,
$\left\{\begin{array}{l}{NM=ND}\\{NG=NH}\end{array}\right.$,
∴Rt△MNH≌Rt△DNG(HL),
∴∠CMQ=∠NDQ,
又∵∠MQC=∠DQN,
∴∠2=∠5=60°,
∵NM=ND,
∴△DMN為等邊三角形;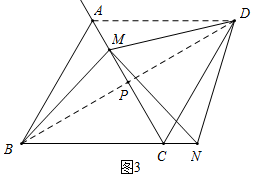
(3)①如圖3,當點M在線段AC上時,連接AD,BD,則BD⊥AC,BP=DP,
∵△ACD和△MND都是等邊三角形,
∴AD=CD,∠ADM=∠CDN,MD=ND,
∴△ADM≌△CDN,
∴AM=CN,
∵$\frac{{S}_{△DMC}}{{S}_{△ABM}}$=3,
∴$\frac{AM}{MC}$=$\frac{1}{3}$,
∴$\frac{CN}{MC}$=$\frac{1}{3}$,
∴$\frac{CN}{CA}$=$\frac{1}{4}$,即$\frac{CN}{CB}$=$\frac{1}{4}$,
∴$\frac{CN}{BN}$=$\frac{1}{5}$,
∴$\frac{{S}_{△MCN}}{{S}_{△MBN}}$=$\frac{1}{5}$;
②如圖4,當點M在CA延長線上時,連接AD,
同理可得,△ADM≌△CDN,
∴AM=CN,
∵$\frac{{S}_{△DMC}}{{S}_{△ABM}}$=3,
∴$\frac{AM}{MC}$=$\frac{1}{3}$,
∴$\frac{AM}{AC}$=$\frac{1}{2}$,即$\frac{CN}{BC}$=$\frac{1}{2}$,
∴BN=CN,
∴$\frac{{S}_{△MCN}}{{S}_{△MBN}}$=1.
綜上所述,$\frac{{S}_{△MCN}}{{S}_{△MBN}}$=$\frac{1}{5}$或1.
故答案為:$\frac{1}{5}$或1.
點評 本題屬于幾何變換綜合題,主要考查了全等三角形的判定與性質、等邊三角形的性質以及含30°角的直角三角形的性質的綜合應用,解決問題的關鍵是作輔助線構造直角三角形和全等三角形,運用全等三角形的對應邊相等,對應角相等進行推導計算.解題時注意分類討論思想的運用.


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
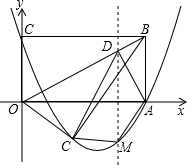 如圖,矩形OABC中,OA=10,OC=5,將其沿對角線OB對折,點C落到點C′處,以點O為坐標原點,OA、OC所在直線為坐標軸,建立如圖所示的平面直角坐標系.
如圖,矩形OABC中,OA=10,OC=5,將其沿對角線OB對折,點C落到點C′處,以點O為坐標原點,OA、OC所在直線為坐標軸,建立如圖所示的平面直角坐標系.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1000 | B. | 1500 | C. | 1800 | D. | 2000 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com