Question

3．如圖1所示，在直角坐標系中，邊長為12的等邊△ABC的邊BC在x軸上，BC邊上的高AD在y軸上，點D與原點O重合，過D點作AB邊的垂線，交AB邊于點E，交AC的延長線于點M．
（1）求證：OC=MC；
（2）將等邊△ABC整體沿x軸的正方向勻速平移，當點B到達原點O時，圖形停止運動．若邊AB與y軸交于點F，請思考并解決以下問題：
①如圖2，延長CA交y軸于點G．如果△ABC平移的速度為每秒1個單位長度，當△AGF與△CDM全等時，平移了多長時間？
②在線段OC上取一點N，連接FN并延長交射線AC于點Q，是否存在一點N，使得CQ=FB？若存在，求線段ON的長；若不存在，說明理由．

Answer 1

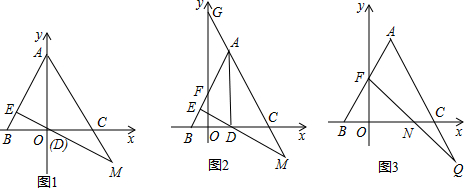
分析 （1）利用等邊三角形的性質得：∠BAC=∠ABC=60°，再利用直角三角形的兩銳角互余得：∠AME=∠COM=30°，所以OC=MC；
（2）①如圖2，設平移t秒時，△AGF≌△CDM，先表示OC的長為6+t，根據30°角所對的直角邊是斜邊的一半列式可求得t的值；
②如圖3，過Q作QH⊥x軸于H，則∠CHQ=90°，證明△BOF≌△CHQ和△FON≌△QHN，得ON=NH、OB=CH，根據等量代換可得結論．

解答 證明：（1）如圖1，∵△ABC是等邊三角形，
∴∠BAC=∠ABC=60°，
∵EM⊥AB，
∴∠AEM=∠BEO=90°，
∴∠AME=90°-60°=30°，∠EOB=90°-60°=30°，
∴∠AME=∠EOB，
∵∠EOB=∠COM，
∴∠AME=∠COM，
∴OC=MC；
（2）①設平移t秒時，△AGF≌△CDM，
則OD=t，
∵△ABC是等邊三角形，AC=BC=12，
∵AD⊥BC，
∴CD=6，
∴AG=CD=6，
在Rt△OGC中，∵∠GCO=60°，
∴∠OGC=30°，
∴CG=2OC，
∴6+12=2（6+t），
t=3；
答：當△AGF與△CDM全等時，平移了3秒；
②如圖3，過Q作QH⊥x軸于H，則∠CHQ=90°，
∵∠QCH=∠ACB=60°，∠ABC=60°，
∴∠ABC=∠QCH，
∵BF=CQ，∠BOF=∠CHQ=90°，
∴△BOF≌△CHQ，
∴FO=HQ，OB=CH，
∵∠FNO=∠QNH，∠FON=∠NHQ=90°，
∴△FON≌△QHN，
∴ON=NH，
∴ON+NH=ON+NC+CH=ON+NC+OB=BC=12，
∴ON=$\frac{1}{2}$BC=6．

點評 本題是三角形的綜合題，考查了等邊三角形、全等三角形的性質和判定及坐標與圖形特點，要熟練掌握全等三角形的判定，要準確判斷出所要證明的邊或角相等是哪兩個三角形全等所得；還利用作輔助線，構建兩三角形全等也是本題的關鍵．