
 如圖,矩形ABCD中,點B與原點重合,點D(8,6),AE⊥BD,△AEB沿著y軸翻折得到△AFB,將△AFB繞著點B順時針旋轉α(0°<α<90°)得到△BF′A′,直線F′A′與線段AB、AE分別交于點M、N,當MN=MA時,△BF′A′與△AEB重疊部分的面積為$\frac{108}{25}$.
如圖,矩形ABCD中,點B與原點重合,點D(8,6),AE⊥BD,△AEB沿著y軸翻折得到△AFB,將△AFB繞著點B順時針旋轉α(0°<α<90°)得到△BF′A′,直線F′A′與線段AB、AE分別交于點M、N,當MN=MA時,△BF′A′與△AEB重疊部分的面積為$\frac{108}{25}$. 分析 依題意畫出圖形,利用相似三角形對應邊成比例求解.
解答 解:在矩形ABCD中,∴AD=8,AB=6,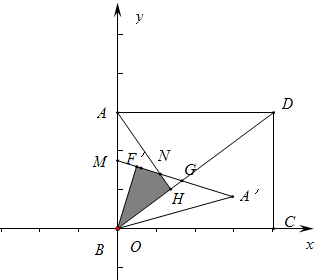
∴DO=$\sqrt{A{B}^{2}+A{D}^{2}}$=10,
∵AE⊥OD,
∴$\frac{1}{2}$•AO•AD=$\frac{1}{2}$•OD•AE,
∴AE=$\frac{24}{5}$,
∴OE=OF′=$\sqrt{A{O}^{2}-A{E}^{2}}$=$\frac{18}{5}$
∵AM=MN,
∴∠MAN=∠ANM,
∵∠ENG+∠NGE=90°,∠ANM=∠ENG,
∴∠AOE=∠OGF′,
∵∠AEO=∠OF′G=90°,
∴△AEO∽△OF′G,
∴$\frac{AE}{OF′}=\frac{AO}{OG}$得OG=$\frac{9}{2}$,
∴F′G=$\sqrt{O{G}^{2}-OF{′}^{2}}$=$\frac{27}{10}$,EG=$\frac{9}{10}$,
由△NEG∽△AEO,得$\frac{NE}{AE}=\frac{EG}{EO}$,
∴NE=$\frac{6}{5}$,
∴S重合=S△OGF′-S△NEG=$\frac{1}{2}$$•\frac{18}{5}$•$\frac{27}{10}$-$\frac{1}{2}$•$\frac{9}{10}$•$\frac{6}{5}$=$\frac{108}{25}$.
故答案為$\frac{108}{25}$.
點評 本題考查了旋轉、矩形的性質、勾股定理、等腰三角形的性質和判定、相似三角形的性質和判定等知識點,解題關鍵是正確畫出圖形,充分利用相似三角形對應邊成比例解決問題.


 同步輕松練習系列答案
同步輕松練習系列答案 課課通課程標準思維方法與能力訓練系列答案
課課通課程標準思維方法與能力訓練系列答案科目:初中數學 來源: 題型:解答題
 如圖,已知在△ABC中,∠A=90°
如圖,已知在△ABC中,∠A=90°查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,把矩形紙片ABCD沿對角線AC折疊,點B落在點E處,P、Q分別是AD、EC的中點,PQ交AE、CD于點M、N,若AB=4,AD=3,求線段MN的長.
如圖,把矩形紙片ABCD沿對角線AC折疊,點B落在點E處,P、Q分別是AD、EC的中點,PQ交AE、CD于點M、N,若AB=4,AD=3,求線段MN的長.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 一班名次 | 二班名次 | 三班名次 | 四班名次 | 五班名次 | |
| 一班班長猜 | 3 | 5 | |||
| 二班班長猜 | 1 | 4 | |||
| 三班班長猜 | 5 | 4 | |||
| 四班班長猜 | 2 | 1 | |||
| 五班班長猜 | 3 | 4 | |||
| 正確結果 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖所示,在寬為20米,長為32米的矩形空地上修的兩條互相垂直的水泥路,余
如圖所示,在寬為20米,長為32米的矩形空地上修的兩條互相垂直的水泥路,余查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 在△ABC中,P、Q分別是BC、AC上的點,作PR⊥AB,垂足分別是R、S,若AQ=PQ,PR=PS,下面四個結論:①PA平分∠BAC,②AS=AR,③QP∥AR,④△BRP≌△CSP中,一定成立的是①②③④(填寫編號即可)
在△ABC中,P、Q分別是BC、AC上的點,作PR⊥AB,垂足分別是R、S,若AQ=PQ,PR=PS,下面四個結論:①PA平分∠BAC,②AS=AR,③QP∥AR,④△BRP≌△CSP中,一定成立的是①②③④(填寫編號即可)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知反比例函數y=$\frac{m-3}{x}$的圖象的一支位于第一象限.
已知反比例函數y=$\frac{m-3}{x}$的圖象的一支位于第一象限.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com