【題目】如圖，
的半徑為
，弦
、
的長度分別為
，則弦
、
所夾的銳角
為________．
【答案】
【解析】
作OE⊥AB于E，OF⊥DC于F，連結OA、OB、OC、OD、BC，根據垂徑定理得BE=
AB=
，CF=DC=，在利用正弦的定義可分別求出∠3=60°，∠4=30°，則根據等腰三角形的性質得∠AOB=2∠3=120°，∠COD=2∠4=60°，然后根據圓周角定理得∠2=60°，∠1=30°，最后利用三角形外角性質求解．
作OE⊥AB于E，OF⊥DC于F，連結OA、OB、OC、OD、BC，如圖所示：
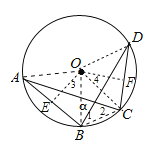
則AE=BE=AB=，CF=DF=DC=，
在Rt△BOE中，BE=，OB=1，
∴sin∠3=，
∴∠3=60°，
在Rt△OCF中，CF=，OC=1，
∴sin∠4=，
∴∠4=30°，
∵OA=OB，OC=OD，
∴∠AOB=2∠3=120°，∠COD=2∠4=60°，
∴∠2=∠AOB=60°，∠1=∠COD=30°
∴∠α=∠1+∠2=90°．
故答案是：90°．
導學教程高中新課標系列答案科目：初中數學 來源： 題型：
【題目】小明參加某個智力競答節目，答對最后兩道單選題就順利通關．第一道單選題有3個選項，第二道單選題有4個選項，這兩道題小明都不會，不過小明還有一個“求助”沒有用（使用“求助”可以讓主持人去掉其中一題的一個錯誤選項）．
（1）如果小明第一題不使用“求助”，那么小明答對第一道題的概率是 ．
（2）如果小明將“求助”留在第二題使用，請用樹狀圖或者列表來分析小明順利通關的概率．
（3）從概率的角度分析，你建議小明在第幾題使用“求助”．（直接寫出答案）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，O為坐標原點，正比例函數
的圖像與反比例函數
的圖像都經過點A（2，m）．
(1)求反比例函數的解析式；
(2)點B在
軸的上，且OA=BA，反比例函數圖像上有一點C，且∠ABC=90°，求點C坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某游泳館推出了兩種收費方式．
方式一：顧客先購買會員卡，每張會員卡200元，僅限本人一年內使用，憑卡游泳，每次游泳再付費30元．
方式二：顧客不購買會員卡，每次游泳付費40元．
設小亮在一年內來此游泳館的次數為x次，選擇方式一的總費用為y1（元），選擇方式二的總費用為y2（元）．
（1）請分別寫出y1，y2與x之間的函數表達式．
（2）若小亮一年內來此游泳館的次數為15次，選擇哪種方式比較劃算？
（3）若小亮計劃拿出1400元用于在此游泳館游泳，采用哪種付費方式更劃算？
查看答案和解析>>
科目：初中數學 來源： 題型：
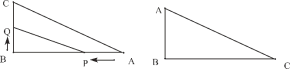
【題目】如圖，在
中，
，
，
，
，
分別是邊
，
上的兩個動點，其中點以每秒2個單位的速度由點
向點
運動；點以每秒3個單位的速度由點到點
再到點運動；它們同時出發，當一個點到達終點停止，另一個點繼續運動到終點也停止，設運動時間為
秒。
（1）求的面積。
（2）當點在邊上運動時，出發幾秒后，
是等腰三角形。
（3）當點在邊
上運動時，出發幾秒后，
是等腰三角形。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，圖①是一個三角形，分別連接三邊中點得圖②，再分別連接圖②中的小三角形三邊中點，得圖③……按此方法繼續下去．
在第
個圖形中有______個三角形（用含的式子表示）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下面材料，完成（1）-（3）題
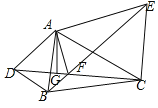
數學課上，老師出示了這樣一道題：如圖，△ABD和△ACE中，AB＝AD，AC＝AE，∠DAB＝∠CAE＝α，連接DC、BE交于點F，過A作AG⊥DC于點G，探究線段FG、FE、FC之間的數量關系，并證明．
同學們經過思考后，交流了自已的想法：
小明：“通過觀察和度量，發現線段BE與線段DC相等．”
小偉：“通過觀察發現，∠AFE與α存在某種數量關系．”
老師：“通過構造全等三角形，從而可以探究出線段FG、FE、FC之間的數量關系．”
（1）求證：BE＝CD；
（2）求∠AFE的度數（用含α的式子表示）；
（3）探究線段FG、FE、FC之間的數量關系，并證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
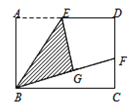
【題目】如圖，矩形ABCD中，E是AD的中點，將△ABE沿BE折疊 得到△GBE，且點G在矩形ABCD內部．將BG延長交DC 于點F，若DC=nDF，則 
=______．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
