Question

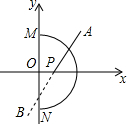
2．如圖，在平面直角坐標系中，以原點O為圓心，3為半徑的半圓，直線AB：y=x+b與x軸交于點P（x，0），若直線AB與半圓弧有公共點，則x值的范圍是（　　）

• A． -3≤x≤3$\sqrt{2}$
• B． -3≤x≤3
• C． -3$\sqrt{2}$≤x≤3
• D． 0≤x≤3$\sqrt{2}$

Answer 1

分析 作OH⊥AB于H，如圖，則OP=|x|，∠OPH=45°，利用等腰直角三角形的性質得OH=$\frac{\sqrt{2}}{2}$|x|，根據題意可判斷直線AB與圓相交或相切，所以$\frac{\sqrt{2}}{2}$|x|≤3，然后解絕對值不等式即可，直線經過點M時OP的值即可．

解答 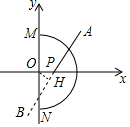解：作OH⊥AB于H，如圖，
∵直線AB：y=x+b，
∴tan∠OHB=$\frac{OB}{OP}$=1，
∴∠OPH=45°
∵OP=|x|，
∴OH=$\frac{\sqrt{2}}{2}$|x|，
∵AB與⊙O有公共點，
∴OH≤3，
即$\frac{\sqrt{2}}{2}$|x|≤3，
當直線與半圓相切時，OP=3$\sqrt{2}$，直線經過M時，OP=3，
∴-3≤x≤3$\sqrt{2}$，
故選A．

點評 本題考查了直線與圓的位置關系：設⊙O的半徑為r，圓心O到直線l的距離為d，若直線l和⊙O相交?d＜r；直線l和⊙O相切?d=r；直線l和⊙O相離?d＞r．解決本題的關鍵是用P點的橫坐標表示點O到直線AB的距離．