
如圖,拋物線y=x2+bx+c與x軸交于A(﹣1,0),B(3,0)兩點.
(1)求該拋物線的解析式;
(2)求該拋物線的對稱軸以及頂點坐標;
(3)設(1)中的拋物線上有一個動點P,當點P在該拋物線上滑動到什么位置時,滿足S△PAB=8,并求出此時P點的坐標.

【考點】待定系數(shù)法求二次函數(shù)解析式;二次函數(shù)的性質(zhì);二次函數(shù)圖象上點的坐標特征.
【分析】(1)由于拋物線y=x2+bx+c與x軸交于A(﹣1,0),B(3,0)兩點,那么可以得到方程x2+bx+c=0的兩根為x=﹣1或x=3,然后利用根與系數(shù)即可確定b、c的值.
(2)根據(jù)S△PAB=8,求得P的縱坐標,把縱坐標代入拋物線的解析式即可求得P點的坐標.
【解答】解:(1)∵拋物線y=x2+bx+c與x軸交于A(﹣1,0),B(3,0)兩點,
∴方程x2+bx+c=0的兩根為x=﹣1或x=3,
∴﹣1+3=﹣b,
﹣1×3=c,
∴b=﹣2,c=﹣3,
∴二次函數(shù)解析式是y=x2﹣2x﹣3.
(2)∵y=﹣x2﹣2x﹣3=(x﹣1)2﹣4,
∴拋物線的對稱軸x=1,頂點坐標(1,﹣4).
(3)設P的縱坐標為|yP|,
∵S△PAB=8,
∴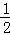 AB•|yP|=8,
AB•|yP|=8,
∵AB=3+1=4,
∴|yP|=4,
∴yP=±4,
把yP=4代入解析式得,4=x2﹣2x﹣3,
解得,x=1±2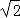 ,
,
把yP=﹣4代入解析式得,﹣4=x2﹣2x﹣3,
解得,x=1,
∴點P在該拋物線上滑動到(1+2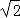 ,4)或(1﹣2
,4)或(1﹣2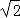 ,4)或(1,﹣4)時,滿足S△PAB=8.
,4)或(1,﹣4)時,滿足S△PAB=8.
【點評】此題主要考查了利用拋物線與x軸的交點坐標確定函數(shù)解析式,二次函數(shù)的對稱軸點的坐標以及二次函數(shù)的性質(zhì),二次函數(shù)圖象上的坐標特征,解題的關鍵是利用待定系數(shù)法得到關于b、c的方程,解方程即可解決問題.


科目:初中數(shù)學 來源: 題型:
在一個不透明的口袋中裝有5個完全相同的小球,把它們分別標號為1,2,3,4,5,從中隨機摸出一個小球,其標號小于4的概率為( )
A.
 B.
B.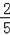
 C.
C.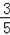
 D.
D.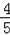

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
在平面直角坐標系中,將拋物線y=x2﹣x﹣6向上(下)或向左(右)平移m個單位,使平移后的拋物線恰好經(jīng)過原點,則|m|的最小值為( )
A.1 B.2 C.3 D.6
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
已知二次函數(shù)y=(m﹣2)x2+(m+3)x+m+2的圖象過點(0,5).
(1)求m值,并寫出二次函數(shù)的解析式.
(2)求y的最小值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
如圖,有一塊矩形紙片ABCD,AB=8,AD=6,將紙片折疊,使得AD邊落在AB邊上,折痕為AE,再將△AED沿DE向右翻折,AE與BC的交點為F,則△CEF的面積為( )
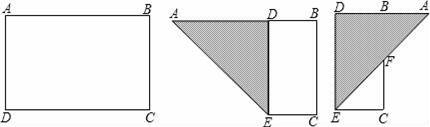

A.
 B.
B.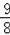
 C.2 D.4
C.2 D.4
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
觀察 下列關于自然數(shù)的等式:
下列關于自然數(shù)的等式:
3 -4×1
-4×1 =5 ①
=5 ①
5 -4×2
-4×2 =9 ②
=9 ②
7 -4×3
-4×3 =13 ③
=13 ③
 根據(jù)上述規(guī)律解決下列問題:
根據(jù)上述規(guī)律解決下列問題:
(1)完成第四個等式:_________________;
(2)寫出你猜想的第n個等式(用含n的式子表示)______________________.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com