Question

14．如圖，△ABC中，AB=AC，tanB=$\frac{1}{2}$，作AD⊥AC交BC于E，且AD=AC，連接CD
（1）若CD=4$\sqrt{2}$，求BE的長度；
（2）如圖2，∠BAD的角平分線交BC于F，作CG⊥AF的反向延長線于點G，求證：$\sqrt{2}$BF+AG=CG；
（3）如圖3，將“tanB=$\frac{1}{2}$”改為“sinB=$\frac{1}{2}$”，作AD⊥AC，且AD=AC，連接BD，CD，延長DA交BC于E，∠BAD的角平分線的反向延長線交BC于F，作CG⊥AF于G，直接寫出$\frac{BF•GC}{BD•BE}$的值．

Answer 1

分析 （1）如圖1中，過A作AF⊥BC于F，根據Rt△ACD中，AC=4，可得Rt△ACE中，AE=2，CE=2$\sqrt{5}$，再根據BC=2CG，求得BC=$\frac{16}{5}\sqrt{5}$，最后根據BE=BC-CE進行計算即可；
（2）如圖2中，連接DF，延長AF交BD于M．首先證明△BFD是等腰直角三角形，再證明△AMD≌△CGA，推出AG=DM=BM=FM，CG=AM，由△BFD是等腰直角三角形，FM⊥BD，推出∠BFM=∠AFN=45°，推出$\sqrt{2}$BF=$\sqrt{2}$AN=AF，由此即可證明；
（3）如圖3中，作AM⊥BC于M，連接DF，FA的延長線交BD于N．首先證明BD=$\sqrt{2}$BF，由sin∠ABC=$\frac{1}{2}$，推出∠ABC=∠ACB=∠EAM=30°，設EM=m，則AE=2m=BE，EC=2AE=4m，AM=FM=$\sqrt{3}$m，CF=CM-FM=3m-$\sqrt{3}$m，CG=$\frac{3m-\sqrt{3}m}{\sqrt{2}}$，由此即可解決問題．

解答 解：（1）如圖1，過A作AF⊥BC于H，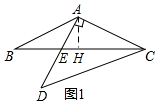

∵AD⊥AC，AD=AC，CD=4$\sqrt{2}$，
∴等腰直角三角形ACD中，AC=4，BC=2CH，
∵AB=AC，tanB=$\frac{1}{2}$，
∴tan∠ACB=$\frac{1}{2}$，
∴Rt△ACE中，AE=2，
∴CE=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$，
∵tan∠ACH=$\frac{1}{2}$，
∴AH=$\frac{4}{5}\sqrt{5}$，CH=$\frac{8}{5}\sqrt{5}$，
∴BC=2×$\frac{8}{5}\sqrt{5}$=$\frac{16}{5}\sqrt{5}$，
∴BE=BC-CE=$\frac{16}{5}\sqrt{5}$-2$\sqrt{5}$=$\frac{6}{5}\sqrt{5}$；

（2）證明：如圖2，連接DF，延長AF交BD于M．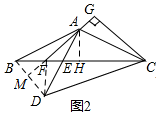

∵AF平分∠BAD，
∴∠FAB=∠FAD，
在△FAB和△FAD中，
$\left\{\begin{array}{l}{AB=AD}\\{∠FAB=∠FAD}\\{AF=AF}\end{array}\right.$，
∴△FAB≌△FAD（SAS），
∴BF=DF，
∴∠DBF=∠FDB=45°，
∴DF⊥BC，
∵AB=AD，MA平分∠BAD，
∴BM=DM，AM⊥BD，
∵∠DAM+∠CAG=90°，∠CAG+∠ACG=90°，
∴∠MAD=∠ACG，
在△AMD和△CGA中，
$\left\{\begin{array}{l}{∠AMD=∠G=90°}\\{∠MAD=∠ACG}\\{AD=AC}\end{array}\right.$，
∴△AMD≌△CGA（AAS），
∴AG=DM=BM=FM，CG=AM，
∵△BFD是等腰直角三角形，FM⊥BD，
∴∠BFM=∠AFH=45°，
∴AH=FH=$\frac{1}{2}$BH，
∴BF=FH=AH，
∴$\sqrt{2}$BF=$\sqrt{2}$AH=AF，
∴CG=AM=FM+AF=AG+$\sqrt{2}$BF，
即$\sqrt{2}$BF+AG=CG；

（3）如圖3，作AM⊥BC于M，連接DF，延長FA交BD于N．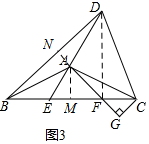

∵AB=AD，AN平分∠BAD，
∴AN⊥BD，BN=DN，
∴FB=FD，
∵AB=AC=AD，
∴∠CBD=$\frac{1}{2}$∠CAD=45°，
∴∠FBD=∠FDB=45°，
∴△BDF是等腰直角三角形，
∴BD=$\sqrt{2}$BF，
∵sin∠ABC=$\frac{1}{2}$，
∴∠ABC=∠ACB=∠EAM=30°，∠BAM=60°，
∵∠BAC=120°，∠DAC=90°，
∴∠BAD=150°，
∴∠BAN=75°，∠MAF=180°-75°-60°=45°=∠AFM，
∴AM=FM，∠GFC=∠GCF=45°，
∴FG=CG，
∵∠AEC=60°，∠ABE=30°，
∴∠ABE=∠BAE=30°，
∴AE=BE，
設EM=m，則AE=2m=BE，EC=2AE=4m，AM=FM=$\sqrt{3}$m，CF=CM-FM=3m-$\sqrt{3}$m，CG=$\frac{3m-\sqrt{3}m}{\sqrt{2}}$，
∴$\frac{BF•GC}{BD•BE}$=$\frac{BF}{\sqrt{2}BF}$•$\frac{\frac{3m-\sqrt{3}m}{\sqrt{2}}}{2m}$=$\frac{3-\sqrt{3}}{4}$．

點評 本題屬于三角形綜合題，主要考查了全等三角形的判定和性質、等腰直角三角形的性質，含30度角的直角三角形的性質以及勾股定理等知識的綜合應用，解題的關鍵是添加輔助線，構造全等三角形和直角三角形，利用含30°角的直角三角形以及等腰直角三角形的邊角關系來解決問題．