
分析 ①由題意可知:a+b=ab=c≠0,將原式變形后將a+b整體代入即可求出答案.
②由題意可知:a=3,b=$\frac{3}{2}$,c=$\frac{9}{2}$,由此即可判斷.
③分別計算(1-a)(1-b)和$\frac{1}{a}$+$\frac{1}{b}$.
④由于a+b=ab=5,聯立方程可知△>0,所以由完全平方公式即可求出a2+b2的值.
解答 解:①∵c≠0,
∴ab≠0
∵a+b=ab,
∴原式=$\frac{a+b-3ab}{2(a+b)+7ab}$=$\frac{ab-3ab}{2ab+7ab}$=$\frac{-2ab}{9ab}$=-$\frac{2}{9}$
故①正確;
②∵a=3,
∴b=$\frac{3}{2}$,c=$\frac{9}{2}$,
∴b+c=6,
故②錯誤;
③∵c≠0,
∴ab≠0,
∵a+b=ab
∴(1-a)(1-b)=1-b-a+ab=1,
$\frac{1}{a}+\frac{1}{b}$=$\frac{a+b}{ab}$=1,
∴(1-a)(1-b)=$\frac{1}{a}$+$\frac{1}{b}$,故③正確;
④∵c=5,
∴a+b=ab=5,
聯立$\left\{\begin{array}{l}{a+b=5}\\{ab=5}\end{array}\right.$,
化簡可得:b2-5b+5=0,
∵△>0,
∴a2+b2=(a+b)2-2ab=15,故④正確
故答案為:①③④
點評 本題考查學生的運算能力,解題的關鍵是熟練運用分式與整式的運算法則,本題屬于中等題型.


科目:初中數學 來源: 題型:填空題
 初三某班學生去中央公園踏青,班級信息員騎自行車先從學校出發,5分鐘后其余同學以60米/分的速度從學校向公園行進,信息員先到達公園后用5分鐘找到聚集地點,再立即按原路以另一速度返回到隊伍匯報聚集地點,最后與同學們一起步行到公園,信息員離其余同學的距離y(米)與信息員出發的時間x(分)之間的關系如圖所示,則信息員開始返回之后,再經過3分鐘與其余同學相距720米.
初三某班學生去中央公園踏青,班級信息員騎自行車先從學校出發,5分鐘后其余同學以60米/分的速度從學校向公園行進,信息員先到達公園后用5分鐘找到聚集地點,再立即按原路以另一速度返回到隊伍匯報聚集地點,最后與同學們一起步行到公園,信息員離其余同學的距離y(米)與信息員出發的時間x(分)之間的關系如圖所示,則信息員開始返回之后,再經過3分鐘與其余同學相距720米.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
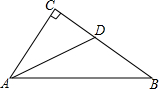 如圖,在△ABC中,∠C=90°,∠CAB的平分線交BC于點D,若AB=5,AC=3,則△DAB的面積為( )
如圖,在△ABC中,∠C=90°,∠CAB的平分線交BC于點D,若AB=5,AC=3,則△DAB的面積為( )| A. | 3 | B. | $\frac{15}{4}$ | C. | 5 | D. | $\frac{25}{8}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
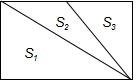 如圖是由三個三角形組成的一個面積為(6a2+4a)cm2的長方形,三個三角形的面積分別是S1,S2,S3,若S1=(3a2+2a)cm2,S3=(2a2-a)cm2,則S2等于(a2+3a)cm2.
如圖是由三個三角形組成的一個面積為(6a2+4a)cm2的長方形,三個三角形的面積分別是S1,S2,S3,若S1=(3a2+2a)cm2,S3=(2a2-a)cm2,則S2等于(a2+3a)cm2.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
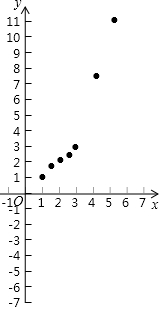 有這樣一個問題:探究函數y=$\frac{1}{2}$(x-1)(x-2)(x-3)+x的性質.
有這樣一個問題:探究函數y=$\frac{1}{2}$(x-1)(x-2)(x-3)+x的性質.| x | … | -$\frac{1}{2}$ | 0 | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | 4 | $\frac{9}{2}$ | … |
| y | … | -$\frac{113}{16}$ | -3 | 1 | $\frac{27}{16}$ | 2 | $\frac{37}{16}$ | 3 | 7 | $\frac{177}{16}$ | … |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 對角線相等的四邊形是矩形 | |
| B. | 對角線互相垂直的四邊形是菱形 | |
| C. | 兩條對角線互相平分且相等的四邊形是正方形 | |
| D. | 順次連接四邊形的各邊中點所得的四邊形是平行四邊形 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com