

分析 (1)求出A、B點(diǎn)的橫坐標(biāo),根據(jù)S△OAB=S△AOC-S△BOC計(jì)算即可.
(2)利用方程組以及根與系數(shù)的關(guān)系,求出AB,根據(jù)AB=$\frac{5}{2}$$\sqrt{2}$,列出方程即可解決問題.
(3)首先證明PM=PF.推出PM+PN=PF+PN≥NF=2推出當(dāng)點(diǎn)P在NF上時(shí)等號成立,此時(shí)NF的方程為y=-x+2$\sqrt{2}$,由(1)知P($\sqrt{2}$-1,$\sqrt{2}$+1),由此即可解決問題.
解答 解答:解:(1)當(dāng)k=-1時(shí),l1:y=-x+2$\sqrt{2}$,
聯(lián)立得,$\left\{\begin{array}{l}{y=-x+2\sqrt{2}}\\{y=\frac{1}{x}}\end{array}\right.$,化簡得x2-2$\sqrt{2}$x+1=0,
解得:x1=$\sqrt{2}$-1,x2=$\sqrt{2}$+1,
設(shè)直線l1與y軸交于點(diǎn)C,則C(0,2$\sqrt{2}$).
S△OAB=S△AOC-S△BOC=$\frac{1}{2}$•2$\sqrt{2}$•(x2-x1)=2$\sqrt{2}$;
(2)根據(jù)題意得:$\left\{\begin{array}{l}{y-\sqrt{2}=k(x-\sqrt{2})}\\{y=\frac{1}{x}}\end{array}\right.$ 整理得:kx2+$\sqrt{2}$(1-k)x-1=0(k<0),
∵△=[$\sqrt{2}$(1-k)]2-4×k×(-1)=2(1+k2)>0,
∴x1、x2 是方程的兩根,
∴$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=\frac{\sqrt{2}(k-1)}{k}}\\{{x}_{1}•{x}_{2}=-\frac{1}{k}}\end{array}\right.$ ①,
∴AB=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$=$\sqrt{({x}_{1}-{x}_{2})^{2}+(\frac{1}{{x}_{1}}-\frac{1}{{x}_{2}})^{2}}$,
=$\sqrt{({x}_{1}-{x}_{2})^{2}[1+(\frac{1}{{x}_{1}{x}_{2}})^{2}]}$,
=$\sqrt{[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}][1+(\frac{1}{{x}_{1}{x}_{2}})^{2}]}$,
將①代入得,AB=$\sqrt{\frac{2({k}^{2}+1)^{2}}{{k}^{2}}}$=$\frac{\sqrt{2}({k}^{2}+1)}{-k}$(k<0),
∴$\frac{\sqrt{2}({k}^{2}+1)}{-k}$=$\frac{5\sqrt{2}}{2}$,
整理得:2k2+5k+2=0,
解得:k=-2,或 k=-$\frac{1}{2}$;
(3)∵y-$\sqrt{2}$=k(x-$\sqrt{2}$)(k<0)過定點(diǎn)F,
∴x=$\sqrt{2}$,y=$\sqrt{2}$,
∴F($\sqrt{2}$,$\sqrt{2}$),
設(shè)P(x,$\frac{1}{x}$),則M(-$\frac{1}{x}$+$\sqrt{2}$,$\frac{1}{x}$),
則PM=x+$\frac{1}{x}$-$\sqrt{2}$=$\sqrt{(x+\frac{1}{x}-\sqrt{2})^{2}}$=$\sqrt{{x}^{2}+\frac{1}{{x}^{2}}-2\sqrt{2}(x+\frac{1}{x})+4}$,
∵PF=$\sqrt{(x-\sqrt{2})^{2}+(\frac{1}{x}-\sqrt{2})^{2}}$=$\sqrt{{x}^{2}+\frac{1}{{x}^{2}}-2\sqrt{2}(x+\frac{1}{x})+4}$,
∴PM=PF.
∴PM+PN=PF+PN≥NF=2,
當(dāng)點(diǎn)P在NF上時(shí)等號成立,此時(shí)NF的方程為y=-x+2$\sqrt{2}$,
由(1)知P($\sqrt{2}$-1,$\sqrt{2}$+1),
∴當(dāng)P($\sqrt{2}$-1,$\sqrt{2}$+1)時(shí),PM+PN最小,此時(shí)四邊形QMPN是周長最小的平行四邊形,
∴Q(-$\sqrt{2}$,2 $\sqrt{2}$).
點(diǎn)評 本題考查反比例函數(shù)綜合題、一次函數(shù)的性質(zhì)、一元二次方程的根與系數(shù)的關(guān)系、兩點(diǎn)間距離公式、平行四邊形的性質(zhì)等知識(shí),解題的關(guān)鍵是學(xué)會(huì)利用方程組求兩個(gè)函數(shù)的交點(diǎn)坐標(biāo)、學(xué)會(huì)利用參數(shù),構(gòu)建方程解決問題,學(xué)會(huì)利用兩點(diǎn)之間線段最短解決最短問題,屬于中考壓軸題.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 9800名學(xué)生是總體 | |
| B. | 每個(gè)學(xué)生是個(gè)體 | |
| C. | 100名學(xué)生是所抽取的一個(gè)樣本 | |
| D. | 100名學(xué)生的視力情況是所抽取的一個(gè)樣本 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,AB是⊙O的直徑,C是半圓O上的一點(diǎn),AC平分∠DAB,AD⊥CD,垂足為D,AD交⊙O于點(diǎn)E,連接CE.
如圖,AB是⊙O的直徑,C是半圓O上的一點(diǎn),AC平分∠DAB,AD⊥CD,垂足為D,AD交⊙O于點(diǎn)E,連接CE.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
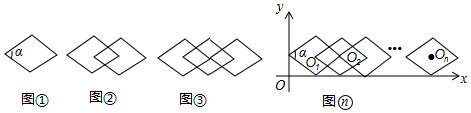
| 圖形名稱 | 基本圖形的個(gè)數(shù) | 菱形的個(gè)數(shù) |
| 圖① | 1 | 1 |
| 圖② | 2 | 3 |
| 圖③ | 3 | 7 |
| 圖④ | 4 | 11 |
| … | … | … |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
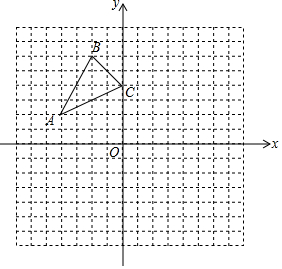 如圖,已知A (-4,2),B (-2,6),C (0,4)是直角坐標(biāo)系平面上三點(diǎn).
如圖,已知A (-4,2),B (-2,6),C (0,4)是直角坐標(biāo)系平面上三點(diǎn).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com