
分析 (1)根據“關聯點”的定義結合點的坐標即可得出結論;
(2)根據點P在函數y=x-1的圖象上,即可得出P(x,x-1)、Q(x,1),再根據點P、Q重合即可得出關于x的一元一次方程,解之即可得出結論;
(3)根據“關聯點”的定義找出點N的坐標,分m≥n和m<n兩種情況考慮,根據點N在函數y=x2的圖象上,即可用含m的代數式表示出n,再根據兩點間的距離公式即可找出MN的關系式,利用一次(二次)函數的性質即可求出線段MN的最大值.
解答 解:(1)∵|2-2|=0,
∴點(2,2)的“關聯點”的坐標為(2,0).
(2)∵點P在函數y=x-1的圖象上,
∴P(x,x-1),則點Q的坐標為(x,1),
∵點Q與點P重合,
∴x-1=1,解得:x=2,
∴點P的坐標為(2,1).
(3)∵點M(m,n),
∴點N(m,|m-n|).
∵點N在函數y=x2的圖象上,
∴|m-n|=m2.
(i)當m≥n時,m-n=m2,
∴n=-m2+m,
∴M(m,-m2+m),N(m,m2).
∵0≤m≤2,
∴MN=|yM-yN|=|-m2+m-m2|=m|2m-1|.
①當0≤m≤$\frac{1}{2}$時,MN=-2m2+m=-2$(x-\frac{1}{4})^{2}$+$\frac{1}{8}$,
∴當m=$\frac{1}{4}$時,MN取最大值,最大值為$\frac{1}{8}$.
②當$\frac{1}{2}$<m≤2時,MN=2m2-m=2$(x-\frac{1}{4})^{2}$+$\frac{1}{8}$,
當m=2時,MN取最大值,最大值為6.
(ii)當m<n時,n-m=m2,
∴n=m2+m,
∴M(m,m2+m),N(m,m2).
∵0≤m≤2,
∴MN=|yM-yN|=|m2+m-m2|=m,
當m=2時,MN取最大值2.
點評 本題考查了二次函數的性質、一次函數的性質、一次函數圖象上點的坐標特征、二次函數圖象上點的坐標特征以及解一元一次方程,解題的關鍵是:(1)根據“關聯點”的定義找出點的關聯點;(2)根據點P、Q重合找出關于x的一元一次方程;(3)用含m的代數式表示出n.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
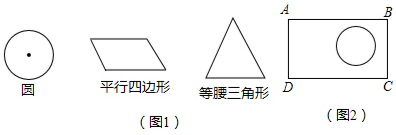
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 運輸工具 | 途中平均速度(千米/時) | 運費(元/千米) | 裝卸費用(元) |
| 火車 | 100 | 15 | 2000 |
| 汽車 | 80 | 20 | 900 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
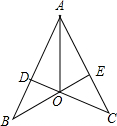 如圖,CD⊥AB,BE⊥AC,垂足分別為D、E,BE與CD相交于點O,且AD=AE,有以下結論:①∠B=∠C,②△ADO≌△AEO;③△BOD≌△COE;④圖中有四組三角形全等,其中正確的結論有( )
如圖,CD⊥AB,BE⊥AC,垂足分別為D、E,BE與CD相交于點O,且AD=AE,有以下結論:①∠B=∠C,②△ADO≌△AEO;③△BOD≌△COE;④圖中有四組三角形全等,其中正確的結論有( )| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 單項式$\frac{1}{2}$xy的系數是$\frac{1}{2}$,次數是1 | |
| B. | 單項式-$\frac{1}{3}$πa2b3的系數是-$\frac{1}{3}$,次數是6 | |
| C. | 單項式x2的系數是1,次數是2 | |
| D. | 多項式2x3-3x2y2+x-1叫三次四項式 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com