
分析 求出∠A=∠BCD,根據銳角三角函數的定義求出sin∠BCD即可.
解答 解: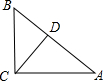
∵CD⊥AB,
∴∠CDB=90°,
由勾股定理得:BC=5,
∵∠ACB=90°,
∴∠A+∠B=90°,∠BCD+∠B=90°,
∴∠A=∠BCD,
∴sinA=sin∠BCD=$\frac{BD}{BC}$=$\frac{3}{5}$,
故答案為:$\frac{3}{5}$.
點評 本題考查了銳角三角函數的定義,能熟記銳角三角函數的定義是解此題的關鍵,注意:在Rt△ACB中,∠ACB=90°,則sinA=$\frac{BC}{AB}$,cosA=$\frac{AC}{AB}$,tanA=$\frac{BC}{AC}$.


 一卷搞定系列答案
一卷搞定系列答案 名校作業本系列答案
名校作業本系列答案 輕巧奪冠周測月考直通名校系列答案
輕巧奪冠周測月考直通名校系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
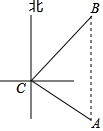 如圖,一艘海輪位于小島C的南偏東60°方向,距離小島120海里的A處,該海輪從A處正北方向航行一段距離后,到達位于小島C北偏東45°方向的B處.
如圖,一艘海輪位于小島C的南偏東60°方向,距離小島120海里的A處,該海輪從A處正北方向航行一段距離后,到達位于小島C北偏東45°方向的B處.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com