
 如圖,在平面直角坐標系中,已知A(9,0),B(0,6),⊙M經過原點O及點A、B.
如圖,在平面直角坐標系中,已知A(9,0),B(0,6),⊙M經過原點O及點A、B.分析 (1)根據圓周角定理∠AOB=90°得AB為⊙M的直徑,則可得到線段AB的中點即點M的坐標,然后利用勾股定理計算出AB,則可確定⊙M的半徑為;
(2)點B作⊙M的切線l交x軸于C,根據切線的性質得AB⊥BC,利用等角的余角相等得到∠BAO=∠CBO,然后根據相似三角形的判定方法有Rt△ABO∽Rt△BCO,可解得OC,則可求得C點坐標為,最后運用待定系數法確定拋物線的解析式;
(3)作ND⊥x軸,連結AE,易得△NOD為等腰直角三角形,再利用ND∥OB得到△ADN∽△AOB,利用相似三角形的性質可求得ND,進一步可求得OD、ON,即可確定N點坐標;由于△ADN∽△AOB,利用相似三角形的性質可求得AN,進一步可求得BN,然后利用圓周角定理得∠OBA=OEA,∠BOE=∠BAE,所以△BON∽△EAN,再利用相似比可求出NE,最后由OE=ON+NE計算即可.
解答 解:
(1)∵∠AOB=90°,
∴AB為⊙M的直徑,
∵A(9,0),B(0,6),
∴OA=9,OB=6,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=3$\sqrt{13}$,
∴⊙M的半徑為$\frac{3\sqrt{13}}{2}$;
∵A(9,0),B(0,6),
∴圓心M的坐標為($\frac{9}{2}$,3);
(2)點B作⊙M的切線l交x軸于C,如圖1,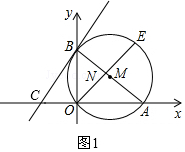
∵BC與⊙M相切,AB為直徑,
∴AB⊥BC,
∴∠ABC=90°,
∴∠CBO+∠ABO=∠ABC=90°,
而∠BAO+∠ABO=90°,
∴∠BAO=∠CBO,
∴Rt△ABO∽Rt△BCO,
∴$\frac{OB}{OC}$=$\frac{OA}{OB}$,即$\frac{6}{OC}$=$\frac{9}{6}$,解得OC=4,
∴C點坐標為(-4,0),
設過A、B、C三點的拋物線解析式為y=ax2+bx+c,
把A、B、C三點的坐標代入可得$\left\{\begin{array}{l}{81a+9b+c=0}\\{16a-4b+c=0}\\{c=6}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{1}{6}}\\{b=\frac{5}{6}}\\{c=6}\end{array}\right.$,
∴拋物線解析式為y=-$\frac{1}{6}$x2+$\frac{5}{6}$x+6;
(3)作ND⊥x軸,連結AE,如圖2,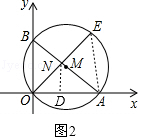
∵∠BOA的平分線交AB于點N,
∴△NOD為等腰直角三角形,
∴ND=OD,
∴ND∥OB,
∴△ADN∽△AOB,
∴ND:OB=AD:AO,
∴ND:6=(9-ND):9,解得ND=$\frac{18}{5}$,
∴OD=$\frac{18}{5}$,ON=$\sqrt{2}$ND=$\frac{18\sqrt{2}}{5}$,
∴N點坐標為($\frac{18}{5}$,$\frac{18}{5}$);
∵△ADN∽△AOB,
∴ND:OB=AN:AB,即$\frac{18}{5}$:6=AN:3$\sqrt{13}$,解得AN=$\frac{9\sqrt{13}}{5}$,
∴BN=3$\sqrt{13}$-$\frac{9\sqrt{13}}{5}$=$\frac{6\sqrt{13}}{5}$,
∵∠OBA=∠OEA,∠BOE=∠BAE,
∴△BON∽△EAN,
∴BN:NE=ON:AN,即$\frac{6\sqrt{13}}{5}$:NE=$\frac{18\sqrt{2}}{5}$:$\frac{9\sqrt{13}}{5}$,解得NE=$\frac{39\sqrt{2}}{10}$,
∴OE=ON+NE=$\frac{18\sqrt{2}}{5}$+$\frac{39\sqrt{2}}{10}$=$\frac{15\sqrt{2}}{2}$.
點評 本題為圓的綜合應用,涉及切線的性質、圓周角定理及其推論、待定系數法、相似三角形的判定和性質、勾股定理等知識點.在(1)中確定出AB為直徑是解題的關鍵,在(2)中利用相似三角形的性質求得點C的坐標是解題的關鍵,在(3)中構造相似三角形分別求得ON、NE的長是解題的關鍵.本題考查知識點較多,綜合性較強,計算量大,難度很大.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | a<m<n<b | B. | m<a<b<n | C. | a<m<b<n | D. | m<a<n<b |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
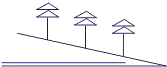 在山坡上植樹,要求兩棵樹間的水平距離是m,測得斜坡的傾斜角為α,則斜坡上相鄰兩棵樹的坡面距離是( )
在山坡上植樹,要求兩棵樹間的水平距離是m,測得斜坡的傾斜角為α,則斜坡上相鄰兩棵樹的坡面距離是( )| A. | $\frac{m}{sinα}$ | B. | $\frac{m}{cosα}$ | C. | m•tanα | D. | m•cosα |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 平方根等于本身的數是0 | |
| B. | 如果a,b都是無理數,那么a+b也一定是無理數 | |
| C. | 坐標平面內的點與有序實數對一一對應 | |
| D. | $\sqrt{12}$與6$\sqrt{\frac{1}{27}}$可以合并同類項 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com