
分析 (1)由面積上的變化關系列出關于m、n的方程組,解之得出m、n的值,再代入可得答案;
(2)根據題意得出m2+n2=3mn,變形可得m2+2mn+n2=5mn,m2-2mn+n2=mn,即(m+n)2=5mn,(m-n)2=mn,從而得出m+n=$\sqrt{5mn}$,m-n=$\sqrt{mn}$,再代入原式=$\frac{{m}^{2}-{n}^{2}}{mn}$=$\frac{(m+n)(m-n)}{mn}$即可得.
解答 解:(1)根據題意知:$\left\{\begin{array}{l}{(m+2)(n+2)-mn=18}\\{(m-1)(n+1)-mn=2}\end{array}\right.$,
整理得$\left\{\begin{array}{l}{m+n=7}\\{m-n=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=5}\\{n=2}\end{array}\right.$,
則原式=$\frac{5}{2}$-$\frac{2}{5}$=$\frac{21}{10}$;
(2)由題意知m2+n2=3mn,
則m2+2mn+n2=5mn,m2-2mn+n2=mn,
即(m+n)2=5mn,(m-n)2=mn,
∵m、n為矩形的邊長,均為正數,
∴m+n=$\sqrt{5mn}$,m-n=$\sqrt{mn}$,
則原式=$\frac{{m}^{2}-{n}^{2}}{mn}$
=$\frac{(m+n)(m-n)}{mn}$
=$\frac{\sqrt{5mn}•\sqrt{mn}}{mn}$
=$\sqrt{5}$.
點評 本題主要考查分式的混合運算、二元一次方程組的應用、完全平方公式等知識點,根據面積上的相等關系列出方程組和對m2+n2=3mn利用完全平方公式變形得出m+n和m-n的值是解題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
| 載重量 | 運往A地的費用 | 運往B地的費用 | |
| 大車 | 15噸/輛 | 630元/輛 | 750元/輛 |
| 小車 | 10噸/輛 | 420元/輛 | 550元/輛 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,直線l1過點A(0,-5),點B(5,0),直線l2與x軸交于點C(-1,0),與y軸交于點D(0,-1),兩直線l1,l2相交于點P,求△PAD的面積是4.
如圖,直線l1過點A(0,-5),點B(5,0),直線l2與x軸交于點C(-1,0),與y軸交于點D(0,-1),兩直線l1,l2相交于點P,求△PAD的面積是4.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
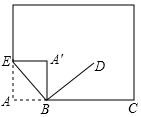 如圖所示,小明將書面折過來,該角頂點A落在A′處,他以折痕BE為一邊作∠DBE=90°,此時小明說BD是∠CBA′的平分線.你認為小明的說法對嗎?說明你的理由.
如圖所示,小明將書面折過來,該角頂點A落在A′處,他以折痕BE為一邊作∠DBE=90°,此時小明說BD是∠CBA′的平分線.你認為小明的說法對嗎?說明你的理由.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com