
 如圖,直線y=-x+3與x、y軸分別交于點A,B,與反比例函數的圖象交于點P(2,1).
如圖,直線y=-x+3與x、y軸分別交于點A,B,與反比例函數的圖象交于點P(2,1).分析 (1)設反比例函數的解析式為y=$\frac{k}{x}$,把點P坐標代入即可解決問題.
(2)如圖,連接AC、BA′、CA′,作CH⊥BA′于H.由sin∠BA′C=$\frac{CH}{CA′}$可知,求出CH、CA′即可解決問題.
解答 解:(1)設反比例函數的解析式為y=$\frac{k}{x}$,
∵反比例函數經過點P(2,1),
∴k=2,
∴y=$\frac{2}{x}$.
(2)如圖,連接AC、BA′、CA′,作CH⊥BA′于H.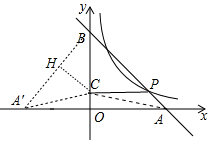
直對于線y=-x+3,令x=0得y=3,令y=0得x=3,
∴A(3,0),B(0,3),
∵PC⊥OB,P(2,1),
∴OC=1,OA=OB=OA′=3,BC=OB-OC=2,
∴S△ABC=$\frac{1}{2}$•BC•OA=$\frac{1}{2}$×2×3=3,
在Rt△OCA′中,CA′=$\sqrt{OA{′}^{2}+O{C}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
在Rt△BOA′中,BA′=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
∵sin∠CBH=$\frac{CH}{BC}$=$\frac{OA′}{BA′}$=$\frac{3}{3\sqrt{2}}$,
∴CH=$\sqrt{2}$,
∴sin∠BA′C=$\frac{CH}{CA′}$=$\frac{\sqrt{2}}{\sqrt{10}}$=$\frac{\sqrt{5}}{5}$.
點評 本題考查反比例函數綜合題、一次函數的應用、銳角三角函數,勾股定理、三角形的面積公式等知識,解題的關鍵是學會添加常用輔助線,構造直角三角形解決問題,屬于中考常考題型.


科目:初中數學 來源: 題型:選擇題
| A. | 我和你相距500米 | |
| B. | 我在你北偏東30°的方向500米處 | |
| C. | 我在你北偏東30°的方向 | |
| D. | 你向北走433米,然后轉90°再走250米 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知:如圖,∠B=∠C=90°,M是BC的中點,且DM平分∠ADC.
已知:如圖,∠B=∠C=90°,M是BC的中點,且DM平分∠ADC.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
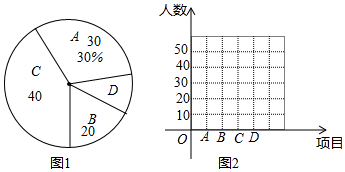
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1或4 | B. | 1或$\frac{1}{4}$ | C. | -1或-4 | D. | -1或-$\frac{1}{4}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 對中央臺“新聞聯播”欄目收視率的調查 | |
| B. | 了解七(3)班同學訂購校服的尺碼情況 | |
| C. | 對一個社區每天丟棄塑料袋數量的調查 | |
| D. | 了解全省中學生每周進行體育鍛煉時間 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com