
 如圖,在△ABC中,∠B=15°,∠C=60°,AC=2,求BC長度.(tan15°=2-$\sqrt{3}$)
如圖,在△ABC中,∠B=15°,∠C=60°,AC=2,求BC長度.(tan15°=2-$\sqrt{3}$) 分析 作輔助線在邊BC上取一點D連接AD,使得AD=BD,作出相應的圖形,根據題意可以求得∠ADC的度數,從而可以得到∠DAC的度數,又由AC=2,可以求出各邊的長,從而可以求得BC的長度.
解答 解:在邊BC上取一點D連接AD,使得AD=BD,如下圖所示: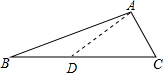
∵AD=BD,∠B=15°
∴∠B=∠BDA=15°,
∴∠ADC=∠B+∠BDA=30°,
∵∠C=60°,AC=2,
∴∠DAC=90°,
∴CD=4,
∴AD=$\sqrt{C{D}^{2}-A{C}^{2}}=\sqrt{{4}^{2}-{2}^{2}}=2\sqrt{3}$,
∴BD=2$\sqrt{3}$,
∴BC=BD+DC=2$\sqrt{3}+4$,
即BC的長度為:$2\sqrt{3}+4$.
點評 本題考查解直角三角形,解題的關鍵作輔助線,構造出直角三角形,然后根據直角三角形的性質求出各邊的長.


科目:初中數學 來源:2017屆湖北省襄陽老河口九年級3月月考數學試卷(解析版) 題型:單選題
下列說法正確的是( )
A. 中位數就是一組數據中最中間的一個數
B. 8,9,9,10,10,11這組數據的眾數是10
C. 如果x1,x2,x3的方差是1,那么2x1,2x2,2x3的方差是4
D. 為了了解生產的一批節能燈的使用壽命,應選擇全面調查
查看答案和解析>>
科目:初中數學 來源:2017屆江蘇省連云港市灌云縣西片九年級下學期第一次月考數學試卷(解析版) 題型:判斷題
在△ABC中,AD是BC邊上的高,∠C=45°,sinB= ,AD=1.則BC的長__.
,AD=1.則BC的長__.

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
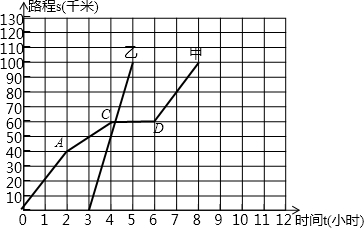
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 3x2-x2=3 | B. | -4xy-2xy=-2xy | C. | x3-x2=x | D. | -0.25ab+$\frac{1}{4}$ba=0 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com