
分析 (1)根據平均單價=$\frac{兩次購買糧食的總金額}{兩次購買糧食的重量和}$,代入可得結論;
(2)先計算張飛兩次購買的糧食重量,再代入平均單價=$\frac{兩次購買糧食的總金額}{兩次購買糧食的重量和}$,計算即可;
(3)利用差比較大小,小的合算.
解答 解:(1)孔明第一次購買糧食付款100x元,第二次購買糧食付款100y元,兩次共付款(100x+100y)元.
∵平均單價=$\frac{兩次購買糧食的總金額}{兩次購買糧食的重量和}$,
∴Q1=$\frac{100x+100y}{100+100}$=$\frac{x+y}{2}$;
(2)張飛第一次購買糧食$\frac{100}{x}$千克,第二次購買糧食$\frac{100}{y}$千克,故兩次共購買糧食$(\frac{100}{x}+\frac{100}{y})$千克,
∵平均單價=$\frac{兩次購買糧食的總金額}{兩次購買糧食的重量和}$,
∴Q2=$\frac{100+100}{\frac{100}{X}+\frac{100}{Y}}$=$\frac{2xy}{x+y}$;
(3)要判斷誰更合算,就是判斷Q1、Q2的大小,小的更合算些,
∵Q1-Q2=$\frac{x+y}{2}$-$\frac{2xy}{x+y}$=$\frac{(x-y)^{2}}{2(x+y)}$,且x≠y,
∴(x-y)2>0而2(x+y)>0,
∴Q1-Q2>0,
故Q1>Q2,
∴張飛的購糧方式更合算.
點評 本題考查了分式的混合運用和實際應用問題,明確平均單價=$\frac{兩次購買糧食的總金額}{兩次購買糧食的重量和}$是本題的關鍵,同時要注意分式大小的比較,方法較多,本題利用了作差比較大小,另外還可以作商、平方法等比較大小.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
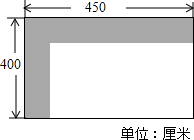 小明家想要在自己家的陽臺上鋪地磚,經測量后設計了如圖的圖紙,黑色區域為寬度相等的一條“7”形的健身用鵝卵石小路,空白部分為地磚鋪設區域.要使鋪地磚的面積為14平方米,那么小路的寬度應為0.5米.
小明家想要在自己家的陽臺上鋪地磚,經測量后設計了如圖的圖紙,黑色區域為寬度相等的一條“7”形的健身用鵝卵石小路,空白部分為地磚鋪設區域.要使鋪地磚的面積為14平方米,那么小路的寬度應為0.5米.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com