
 如圖,一次函數y=ax-2(a≠0)的圖象與反比例函數y=$\frac{k}{x}$(k≠0)的圖象交于第二象限的點,且與x軸、y軸分別交于點C、D.已知tan∠AOC=$\frac{1}{3}$,AO=$\sqrt{10}$.
如圖,一次函數y=ax-2(a≠0)的圖象與反比例函數y=$\frac{k}{x}$(k≠0)的圖象交于第二象限的點,且與x軸、y軸分別交于點C、D.已知tan∠AOC=$\frac{1}{3}$,AO=$\sqrt{10}$.分析 (1)先過點A作AE⊥x軸于E,構造Rt△AOE,再根據tan∠AOC=$\frac{1}{3}$,AO=$\sqrt{10}$,求得AE=1,OE=3,即可得出A(-3,1),進而運用待定系數法,求得一次函數和反比例函數的解析式;
(2)先點F是點D關于x軸的對稱點,求得F(0,2),再根據解方程組求得B(1,-3),最后根據△ABF的面積=△ADF面積+△BDF面積,進行計算即可.
解答 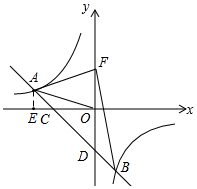 解:(1)過點A作AE⊥x軸于E,
解:(1)過點A作AE⊥x軸于E,
∵tan∠AOC=$\frac{1}{3}$,AO=$\sqrt{10}$,
∴Rt△AOE中,AE=1,OE=3,
∵點A在第二象限,
∴A(-3,1),
∵反比例函數y=$\frac{k}{x}$(k≠0)的圖象過點A,
∴k=-3×1=-3,
∴反比例函數的解析式為y=-$\frac{3}{x}$,
∵一次函數y=ax-2(a≠0)的圖象過點A,
∴1=-3a-2,
解得a=-1,
∴一次函數的解析式為y=-x-2;
(2)一次函數的解析式y=-x-2中,令x=0,則y=-2,
∴D(0,-2),
∵點F是點D關于x軸的對稱點,
∴F(0,2),
∴DF=2+2=4,
解方程組$\left\{\begin{array}{l}{y=-x-2}\\{y=-\frac{3}{x}}\end{array}\right.$,可得$\left\{\begin{array}{l}{x=-3}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=-3}\end{array}\right.$,
∴B(1,-3),
∵△ADF面積=$\frac{1}{2}$×DF×CE=6,
△BDF面積=$\frac{1}{2}$×DF×|xB|=2,
∴△ABF的面積=△ADF面積+△BDF面積=6+2=8.
點評 本題主要考查了反比例函數與一次函數交點問題,解決問題的關鍵是運用待定系數法求得一次函數和反比例函數的解析式.解題時注意:求正比例函數,只要一對x,y的值就可以;而求一次函數y=kx+b,則需要兩組x,y的值.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:解答題
 如圖,點A是第一象限內的點,坐標為(4,y),OA與x軸正半軸的夾角α的正弦角α的正弦值為$\frac{3}{5}$,求點A的坐標及α的余弦值.
如圖,點A是第一象限內的點,坐標為(4,y),OA與x軸正半軸的夾角α的正弦角α的正弦值為$\frac{3}{5}$,求點A的坐標及α的余弦值.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 日期 | 天氣 |
| 9月15日 | 晴 |
| 9月16日 | 陰 |
| 9月17日 | 陰 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
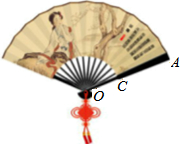 中國扇文化有著深厚的文化底蘊,是民族文化的一個組成部分,它與竹文化、佛教文化有著密切關系.歷來中國被譽為制扇王國.扇子主要材料是:竹、木、紙、象牙、玳瑁、翡翠、飛禽翎毛、其它棕櫚葉、檳榔葉、麥桿、蒲草等也能編制成各種千姿百態的日用工藝扇,造型優美,構造精制,經能工巧匠精心鏤、雕、燙、鉆或名人揮毫題詩作畫,使扇子藝術身價倍增.折扇,古稱“聚頭扇“,或稱為撒扇,或折疊扇,以其收攏時能夠二頭合并歸一而得名.如圖,折扇的骨柄OA的長為5a,扇面的寬CA的長為3a,折扇張開的角度為n°,求出扇面的面積(用代數式表示).
中國扇文化有著深厚的文化底蘊,是民族文化的一個組成部分,它與竹文化、佛教文化有著密切關系.歷來中國被譽為制扇王國.扇子主要材料是:竹、木、紙、象牙、玳瑁、翡翠、飛禽翎毛、其它棕櫚葉、檳榔葉、麥桿、蒲草等也能編制成各種千姿百態的日用工藝扇,造型優美,構造精制,經能工巧匠精心鏤、雕、燙、鉆或名人揮毫題詩作畫,使扇子藝術身價倍增.折扇,古稱“聚頭扇“,或稱為撒扇,或折疊扇,以其收攏時能夠二頭合并歸一而得名.如圖,折扇的骨柄OA的長為5a,扇面的寬CA的長為3a,折扇張開的角度為n°,求出扇面的面積(用代數式表示).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com