
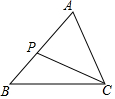
 如圖,已知在△ABC中,P為AB上一點,連接CP,以下條件中不能判定△ACP∽△ABC的是( )
如圖,已知在△ABC中,P為AB上一點,連接CP,以下條件中不能判定△ACP∽△ABC的是( )| A. | ∠ACP=∠B | B. | ∠APC=∠ACB | C. | $\frac{AC}{AB}=\frac{CP}{BC}$ | D. | $\frac{AC}{AP}=\frac{AB}{AC}$ |
分析 A、加一公共角,根據兩角對應相等的兩個三角形相似可以得結論;
B、加一公共角,根據兩角對應相等的兩個三角形相似可以得結論;
C、其夾角不相等,所以不能判定相似;
D、其夾角是公共角,根據兩邊的比相等,且夾角相等,兩三角形相似.
解答 解:A、∵∠A=∠A,∠ACP=∠B,
∴△ACP∽△ABC,
所以此選項的條件可以判定△ACP∽△ABC;
B、∵∠A=∠A,∠APC=∠ACB,
∴△ACP∽△ABC,
所以此選項的條件可以判定△ACP∽△ABC;
C、∵$\frac{AC}{AB}=\frac{CP}{BC}$,
當∠ACP=∠B時,△ACP∽△ABC,
所以此選項的條件不能判定△ACP∽△ABC;
D、∵$\frac{AC}{AP}=\frac{AB}{AC}$,
又∠A=∠A,
∴△ACP∽△ABC,
所以此選項的條件可以判定△ACP∽△ABC,
本題選擇不能判定△ACP∽△ABC的條件,
故選C.
點評 本題考查了相似三角形的判定,熟練掌握相似三角形的判定方法是關鍵.


 期末集結號系列答案
期末集結號系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
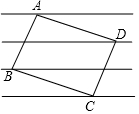 如圖,矩形ABCD的四個頂點正好落在四條平行線上,并且從上到下每兩條平行線間的距離都是1,如果AB:BC=3:4,那么AB的長是$\frac{\sqrt{73}}{4}$.
如圖,矩形ABCD的四個頂點正好落在四條平行線上,并且從上到下每兩條平行線間的距離都是1,如果AB:BC=3:4,那么AB的長是$\frac{\sqrt{73}}{4}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com