
分析 (1)根據(jù)給定的新定義,代入數(shù)據(jù)即可得出結(jié)論;
(2)分a-b-c≥0和a-b-c≤0兩種情況考慮,分別代入定義式中找出最大值,比較后即可得出結(jié)論.
解答 解:(1)根據(jù)題中的新定義得:
3⊕(-2)⊕(-3),
=$\frac{1}{2}$(|3-(-2)-(-3)|+3+(-2)+(-3)),
=$\frac{1}{2}$(8-2),
=3.
(2)當(dāng)a-b-c≥0時(shí),
原式=$\frac{1}{2}$(a-b-c+a+b+c)=a,
此時(shí)最大值為a=$\frac{8}{9}$;
當(dāng)a-b-c≤0時(shí),
原式=$\frac{1}{2}$(-a+b+c+a+b+c)=b+c,
此時(shí)最大值為b+c=$\frac{7}{9}$+$\frac{8}{9}$=$\frac{5}{3}$.
∵$\frac{5}{3}$>$\frac{8}{9}$,
∴計(jì)算結(jié)果的最大值為$\frac{5}{3}$.
點(diǎn)評 本題考查了有理數(shù)的混合運(yùn)算,讀懂題意弄清新定義式的運(yùn)算是解題的關(guān)鍵.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
 如圖,四邊形ABCD內(nèi)接于⊙O,AD、BC的延長線相交于點(diǎn)E,AB、DC的延長線相交于點(diǎn)F,∠A=50°,則∠E+∠F=80°.
如圖,四邊形ABCD內(nèi)接于⊙O,AD、BC的延長線相交于點(diǎn)E,AB、DC的延長線相交于點(diǎn)F,∠A=50°,則∠E+∠F=80°.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | -a2•(-a3)=a6 | B. | (a2)-3=a-6 | C. | ($\frac{1}{a+1}$)-2=-a2-2a-1 | D. | (2a+1)0=1 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
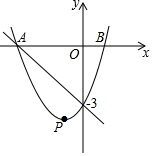 已知二次函數(shù)的圖象經(jīng)過點(diǎn)(0,-3),(2,5),(-1,-4)且與x軸交于A、B兩點(diǎn),其頂點(diǎn)為P.
已知二次函數(shù)的圖象經(jīng)過點(diǎn)(0,-3),(2,5),(-1,-4)且與x軸交于A、B兩點(diǎn),其頂點(diǎn)為P.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
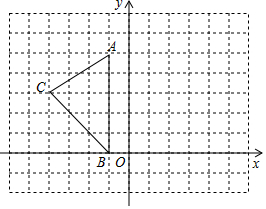 已知:如圖,已知△ABC,
已知:如圖,已知△ABC,查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 4個 | B. | 3個 | C. | 2個 | D. | 1個 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com