

分析 (1)根據同角的余角相等可以得:∠ABD=∠NAC;
(2)如圖2作輔助線,構建全等三角形,利用ASA證明△ECN≌△PCN,得∠APC=∠NEC,再利用SAS證明△ECN≌△PCN,所以∠APC=∠NEC,則∠ADB=∠NEC,利用等角對等邊得:FD=FE;
(3)如圖1,同理可證明FD=FE,則△FED為等腰三角形.
解答  解:(1)如圖1,∵∠BAC=90°,
解:(1)如圖1,∵∠BAC=90°,
∴∠NAC+∠BAN=90°,
∵AM⊥BD,
∴∠AMB=90°,
∴∠ABD+∠BAN=90°,
∴∠ABD=∠NAC;
(2)FD=FE,理由是:
如圖2,過C作CP⊥AC,交AN的延長線于P,
∴∠ACP=∠BAC=90°,
∵AB=AC,∠NAC=∠ABD,
∴△APC≌△BDA,
∴AD=PC,∠ADB=∠APC,
由題意得:AD=EC,
∴AD=EC=PC,
∵AB=AC,∠BAC=90°,
∴∠ACB=45°,
∴∠PCN=45°,
∴∠ACB=∠PCN,
∵NC=NC,
∴△ECN≌△PCN,
∴∠APC=∠NEC,
∴∠ADB=∠NEC,
∴FD=FE;
(3)如圖1,過C作CP⊥AC,交AN的延長線于P,
∴∠ACP=∠BAC=90°,
∵AB=AC,∠NAC=∠ABD,
∴△APC≌△BDA,
∴AD=PC,∠ADB=∠APC,
由題意得:AD=EC,
∴AD=EC=PC,
∵AB=AC,∠BAC=90°,
∴∠ACB=45°,
∴∠PCN=45°,
∴∠ACB=∠PCN,
∵NC=NC,
∴△ECN≌△PCN,
∴∠APC=∠NEC,
∴∠ADB=∠NEC,
∵∠ADB=∠FDE,∠NEC=∠FED,
∴∠FDE=∠FED,
∴FD=FE;
∴△FED為等腰三角形.
點評 本題是三角形的綜合題,考查了等腰直角三角形、等腰三角形、全等三角形的性質和判定,本題主要利用證明兩個三角形全等來證明邊相等或角相等,從而解決問題.


科目:初中數學 來源: 題型:解答題

| 圖形編號 | (1) | (2) | (3) | (4) | … | (10) | … | (100) |
| 圖中座位總數 | 6 | 10 | 14 | 18 | … | 42 | … | 402 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
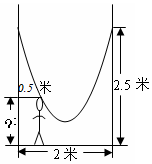 如圖,小明的父親在相距2米的兩棵樹間拴了一根繩子,給小明做了一個簡易的秋千.拴繩子的地方距地面高都是2.5米,繩子自然下垂呈拋物線狀,身高1米的小明距較近的那棵樹0.5米時,頭部剛好接觸到繩子,則繩子的最低點距地面的距離為多少米?
如圖,小明的父親在相距2米的兩棵樹間拴了一根繩子,給小明做了一個簡易的秋千.拴繩子的地方距地面高都是2.5米,繩子自然下垂呈拋物線狀,身高1米的小明距較近的那棵樹0.5米時,頭部剛好接觸到繩子,則繩子的最低點距地面的距離為多少米?查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com