
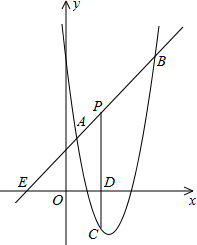
 如圖,直線y=x+2與拋物線y=ax2+bx+6(a≠0)相交于A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),點(diǎn)P是線段AB上異于A、B的動(dòng)點(diǎn),過點(diǎn)P作PC⊥x軸于點(diǎn)D,交拋物線于點(diǎn)C.
如圖,直線y=x+2與拋物線y=ax2+bx+6(a≠0)相交于A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),點(diǎn)P是線段AB上異于A、B的動(dòng)點(diǎn),過點(diǎn)P作PC⊥x軸于點(diǎn)D,交拋物線于點(diǎn)C.分析 (1)根據(jù)題意可以求得m的值,從而可以求得a、b的值,從而可以求得拋物線的解析式;
(2)根據(jù)△PAC為直角三角形,可以得到PA⊥AC或PC⊥AC,然后針對(duì)兩種情況分別求出點(diǎn)P的坐標(biāo)即可解答本題.
解答 解:(1)∵點(diǎn)A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m)在直線y=x+2上,
∴當(dāng)x=4時(shí),y=4+2=6,
∴m=6,
即點(diǎn)B的坐標(biāo)為(4,6),
∵點(diǎn)A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,6)在拋物線y=ax2+bx+6(a≠0)上,
∴$\left\{\begin{array}{l}{a×(\frac{1}{2})^{2}+b×\frac{1}{2}+6=\frac{5}{2}}\\{a×{4}^{2}+b×4+6=6}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{a=2}\\{b=-8}\end{array}\right.$,
即拋物線的解析式為:y=2x2-8x+6;
(2)∵△PAC為直角三角形,
∴PA⊥AC或PC⊥AC,
當(dāng)PA⊥AC時(shí),
∵點(diǎn)P是線段AB上異于A、B的動(dòng)點(diǎn),過點(diǎn)P作PC⊥x軸于點(diǎn)D,交拋物線于點(diǎn)C,
∴設(shè)點(diǎn)C的坐標(biāo)為(m,2m2-8m+6),
將x=m代入y=x+2得,y=m+2,
∴點(diǎn)P的坐標(biāo)為(m,m+2),
∵點(diǎn)A($\frac{1}{2}$,$\frac{5}{2}$),點(diǎn)P(m,m+2),點(diǎn)C(m,2m2-8m+6),
∴$\frac{m+2-\frac{5}{2}}{m-\frac{1}{2}}•\frac{2{m}^{2}-8m+6-\frac{5}{2}}{m-\frac{1}{2}}=-1$,
解得,${m}_{1}=\frac{1}{2}$(舍去),m2=3,
∴點(diǎn)P(3,5);
當(dāng)PC⊥AC時(shí),
∵點(diǎn)A($\frac{1}{2}$,$\frac{5}{2}$),
∴點(diǎn)C的縱坐標(biāo)為$\frac{5}{2}$,
將y=$\frac{5}{2}$代入y=2x2-8x+6,得${x}_{1}=\frac{1}{2},{x}_{2}=\frac{7}{2}$,
∴此時(shí)點(diǎn)C的坐標(biāo)為($\frac{7}{2},\frac{5}{2}$),
將x=$\frac{7}{2}$代入y=x+2,得y=$\frac{11}{2}$,
即點(diǎn)P的坐標(biāo)為($\frac{7}{2},\frac{11}{2}$);
由上可得,當(dāng)△PAC為直角三角形時(shí)點(diǎn)P的坐標(biāo)為(3,5)或($\frac{7}{2},\frac{11}{2}$).
點(diǎn)評(píng) 本題考查二次函數(shù)綜合題,解答此類問題的關(guān)鍵是明確待定系數(shù)法求二次函數(shù)解析式的方法,會(huì)用分類討論的數(shù)學(xué)思想和數(shù)形結(jié)合的數(shù)學(xué)思想解答問題,



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 1個(gè) | B. | 2個(gè) | C. | 3個(gè) | D. | 4個(gè) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{5}{2}$ x2y與-$\frac{3}{2}$ xy3 | B. | -8a2b與5a2c | C. | $\frac{1}{4}$ pq與-$\frac{5}{2}$ qp | D. | 19abc與-28ab |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
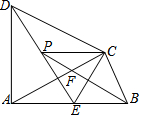 如圖,四邊形ABCD中,AD=DC,∠DAB=∠ACB=90°,過點(diǎn)D作DF⊥AC,垂足為F,DF與AB相交于E.若AB=25,BC=15,P是射線DF上的動(dòng)點(diǎn).當(dāng)△BCP的周長最小時(shí),DP的長為$\frac{125}{6}$.
如圖,四邊形ABCD中,AD=DC,∠DAB=∠ACB=90°,過點(diǎn)D作DF⊥AC,垂足為F,DF與AB相交于E.若AB=25,BC=15,P是射線DF上的動(dòng)點(diǎn).當(dāng)△BCP的周長最小時(shí),DP的長為$\frac{125}{6}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
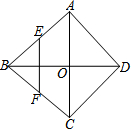 如圖,菱形ABCD的對(duì)角線AC、BD相交于O點(diǎn),E、F分別是AB、BC邊上的中點(diǎn),連接EF.若EF=$\sqrt{3}$,BD=4,則菱形ABCD的周長為( )
如圖,菱形ABCD的對(duì)角線AC、BD相交于O點(diǎn),E、F分別是AB、BC邊上的中點(diǎn),連接EF.若EF=$\sqrt{3}$,BD=4,則菱形ABCD的周長為( )| A. | 5 | B. | $4\sqrt{6}$ | C. | $4\sqrt{7}$ | D. | 20 |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com