
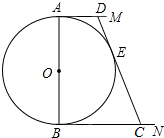
 如圖,⊙O的直徑AB=6,AM和BN是它的兩條切線,DC與⊙O相切于點E,并與AM、BN分別相交于D、C兩點,當1≤BC≤3時,AD的取值范圍是3≤AD≤9.
如圖,⊙O的直徑AB=6,AM和BN是它的兩條切線,DC與⊙O相切于點E,并與AM、BN分別相交于D、C兩點,當1≤BC≤3時,AD的取值范圍是3≤AD≤9. 分析 連接OD、OE、OC,根據切線長定理可知DO、CO平分∠ADC、∠DCB,從而可知∠DOC=90°,然后證明△ODE∽△COE,利用相似三角形的性質即可求出OE2=CE•DE.
解答 解:∵ AM、BN、CD是⊙O的兩條切線,
AM、BN、CD是⊙O的兩條切線,
∴DO、CO分別平分∠ADC、∠DCB,
AD=DE,BC=CE
∴∠ODC+∠OCD=$\frac{1}{2}$(∠ADC+∠DCB)
∵AD∥BC,
∴∠ODC+∠OCD=90°,
∴∠DOC=90°,
∵OE⊥CD,
∴∠DOE+∠COE=∠COE+∠OCE=90°
∴∠DOE=∠OCE
∴△ODE∽△OCE
∴OE2=CE•ED
∵OE=$\frac{1}{2}$AB=3,
∴9=CE•ED=AD•BC
∴AD=$\frac{9}{BC}$
∵1≤BC≤3
∴3≤AD≤9
故答案為:3≤AD≤9
點評 本題考查切線長的性質,解題的關鍵是連接OE、OC、OD證明△ODE∽△COE,本題屬于中等題型.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:初中數學 來源: 題型:解答題
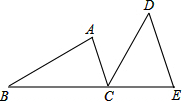 如圖,B、C、E三點在同一條直線上,AC∥DE,AC=CE,∠ACD=∠B.
如圖,B、C、E三點在同一條直線上,AC∥DE,AC=CE,∠ACD=∠B.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com