
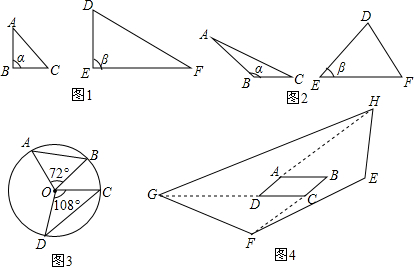
分析 (1)①②根據(jù)共角三角形的定義,可得答案;
(2)根據(jù)同角的補角相等,可得:∠ABM=∠E,根據(jù)相似三角形的判定,可得△ABM∽△DEN,根據(jù)相似三角形的性質(zhì),可得對應(yīng)邊的比相等,可得證明的結(jié)論;
(3)根據(jù)共角三角形面積的關(guān)系,可得答案;
(4)根據(jù)共角三角形面積的關(guān)系,可得共角三角形的面積,根據(jù)面積的和差,可得答案..
解答 解:(1)根據(jù)共角三角形的定義可知①對 ②錯;
故答案為對,錯.
(2)③證明:如圖2中,過A作AM⊥BC交BC的延長線于點M、過D作DN⊥EF于點N,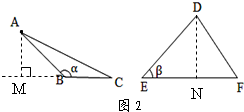
∴∠AMB=∠DNE=90°
又∵∠ABM+α=β+α=180°
∴∠ABM=β
即:∠ABM=∠E
∴△ABM∽△DEN
∴$\frac{AM}{DN}$=$\frac{AB}{DE}$,
∴$\frac{{S}_{△ABC}}{{S}_{△DEF}}$=$\frac{\frac{1}{2}AM•BC}{\frac{1}{2}DN•EF}$=$\frac{AM}{DN}$•$\frac{BC}{EF}$=$\frac{AB}{DE}$•$\frac{BC}{EF}$=$\frac{AB•BC}{DE•EF}$;
(3)如圖3中,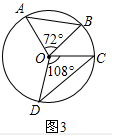
∵△OAB與△OCD是共角三角形,OA=OB=OC=OD,
∴$\frac{{S}_{△OAB}}{{S}_{△OCD}}$=$\frac{{S}_{1}}{{S}_{2}}$=$\frac{OA•OB}{OC•OD}$=1,
∴S1=S2;
故答案為:S1=S2.
(4)如圖4中,連接AC、BD.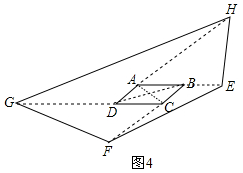
四邊形ABCD的面積為2,
S△ABC=S△ADC=S△BAD=S△BCD=1,
使BE=AB,CF=2BC,DG=2CD,AH=3AD,
由共角三角形的面積比等于對應(yīng)角兩邊的乘積之比得
$\frac{{S}_{△BEF}}{{S}_{△ABC}}$=$\frac{BE•EF}{AB•BC}$=$\frac{AB•3BC}{AB•BC}$=3,S△BEF=3,
$\frac{{S}_{△GCF}}{{S}_{△BCD}}$=$\frac{CG•CF}{CB•CD}$=$\frac{3CD•2BC}{CD•BC}$=6,S△GCF=6,
$\frac{{S}_{△HDG}}{{S}_{△ADC}}$=$\frac{DG•DH}{DA•DC}$=$\frac{2CD•4DA}{CD•DA}$=8,S△DGH=8,
$\frac{{S}_{△AHE}}{{S}_{△ADB}}$=$\frac{AH•AE}{AD•AB}$ $\frac{3AD•2AB}{AD•AB}$═6,S△AHE=6,
SEFGH=S△BEF+S△GCF+S△DGH+S△AHE+SABCD
=3+6+8+6+2=25,
故答案為25.
點評 本題考查了圓的綜合題,共角三角形的面積之間的關(guān)系是解題關(guān)鍵.


科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖,要設(shè)計一幅寬20cm,長30cm的圖案,其中有兩橫兩豎的彩條,橫豎彩條的寬度比為2:1,如果要使彩條所占面積是圖案面積的$\frac{19}{75}$,則豎彩條寬度為( )
如圖,要設(shè)計一幅寬20cm,長30cm的圖案,其中有兩橫兩豎的彩條,橫豎彩條的寬度比為2:1,如果要使彩條所占面積是圖案面積的$\frac{19}{75}$,則豎彩條寬度為( )| A. | 1cm | B. | 1.5cm | C. | 2cm | D. | 2.5cm |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
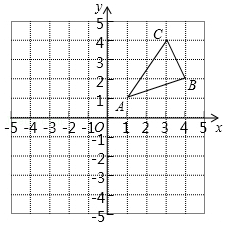 如圖,△ABC三個頂點的坐標(biāo)分別為A(1,1),B(4,2),C(3,4).
如圖,△ABC三個頂點的坐標(biāo)分別為A(1,1),B(4,2),C(3,4).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖,△ABC為等邊三角形,且BM=CN,AM與BN相交于點P,則∠APN=( )
如圖,△ABC為等邊三角形,且BM=CN,AM與BN相交于點P,則∠APN=( )| A. | 70° | B. | 60° | C. | 50° | D. | 大小不確定 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com