
分析 (1)連接BF,根據圓周角定理得到∠CBF=∠BAF,∠ABC=90°,等量代換得到∠BAD=∠DAF+∠BAF=∠ABF+∠CBF=∠ABC=90°,即可得到結論;
(2)連接BF,由(1)的結論推出四邊形ABCD是正方形,得到tan∠DAG=$\frac{1}{2}$,設正方形ABCD的各邊長為2a,求得tan∠ABF=$\frac{1}{2}$,根據勾股定理得到AG=$\sqrt{5}$a,求得tan∠CFG=$\frac{1}{2}$即可得到結論;
(3)連接AP,BF,由AB是⊙O的直徑,得到AP⊥BL,根據AB是⊙O的直徑,得到BP⊥AI,求得tan∠ABF=tan∠DAG=tan∠IBF=$\frac{1}{2}$,得到tan∠LAP=tan∠BAP=$\frac{1}{3}$,根據已知條件得到∠PAB=∠KAD,設BK與⊙O交于H,連接AH,過K作KK?⊥AB解三角形得到AH=$\frac{4\sqrt{10}}{5}$,BH=$\frac{3\sqrt{10}}{5}$,根據相似三角形的性質得到$\frac{AH}{KK′}$=$\frac{BH}{BK′}$,求得AK′=$\frac{4\sqrt{10}}{5}$,KK′=$\frac{12\sqrt{10}}{5}$,于是得到結論.
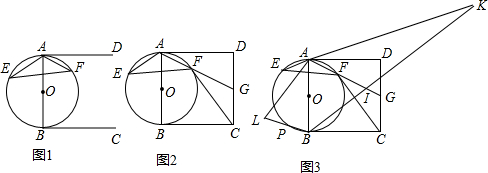
解答 解: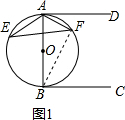 (1)連接BF,如圖1所示:
(1)連接BF,如圖1所示:
∵AB是⊙O的直徑,BC是⊙O的切線,
∴∠CBF=∠BAF,∠ABC=90°,
∵∠AEF=∠ABF,∠DAF=∠AEF,
∴∠ABF=∠DAF,
∴∠BAD=∠DAF+∠BAF=∠ABF+∠CBF=∠ABC=90°,
∴AD∥BC;
(2)如圖2,連接BF,
由(1)知:∠BAD=∠ABC=90°,AD∥BC,
∵AD=BC=AB,
∴四邊形ABCD是正方形,
∵G為CD中點,
∴tan∠DAG=$\frac{1}{2}$,
∵∠ABF=∠DAF,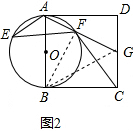
∴tan∠ABF=$\frac{1}{2}$,
∵∠BFG=∠BCD=90°,
∴B,C,G,F四點共圓,
∴∠CFG=∠CBG,
∵tan∠CBG=$\frac{CG}{BC}=\frac{1}{2}$,
∴tan∠CFG=$\frac{1}{2}$,
∴∠CFG=∠ABF,∠CFB=∠CBF,
∴CB=CF;
(3)如圖3,連接AP,BF,
∵AB是⊙O的直徑,
∴AP⊥BL,
∵LP=BP,
∴∠LAP=∠BAP,
∵AB是⊙O的直徑,
∴BP⊥AI,
∵IF=AF,
∴∠ABF=∠IBF,
∴tan∠ABF=tan∠DAG=tan∠IBF=$\frac{1}{2}$,
又∵∠ABI+∠BAL=90°,
∴∠LAP+∠BAP=45°,
∴tan(∠LAP+∠BAP)=$\frac{tan∠LAP+tan∠BAP}{1-tan∠LAP•tan∠BAP}$=1,
tan∠LAP=tan∠BAP=$\frac{1}{3}$,
∵∠BAK+∠ABL=180°,
∴∠BAK+90°-∠PAB=180°,
∴∠BAK=90°+∠PAB,
又∴∠BAK=90°+∠KAD,
∴∠PAB=∠KAD,
設BK與⊙O交于H,連接AH,過K作KK?⊥AB,
∵tan∠ABF=$\frac{1}{2}$,AB=$\sqrt{10}$,
∴BF=AI=2$\sqrt{2}$,
∵AB=BI,
∴AH=$\frac{4\sqrt{10}}{5}$,BH=$\frac{3\sqrt{10}}{5}$,
∵△ABH∽△BKK′,
∴$\frac{AH}{KK′}$=$\frac{BH}{BK′}$,
∵KK′∥AD,
∴∠K′KA=∠DAK=∠BAP,
∴$\frac{AK′}{KK′}$=$\frac{1}{3}$,
∴AK′=$\frac{4\sqrt{10}}{5}$,
∴KK′=$\frac{12\sqrt{10}}{5}$,
∴S四邊形ALBF=S△ALB+S△ABK=$\frac{1}{2}$BL•AP+$\frac{1}{2}$AB•KK′=3+12=15.
點評 本題考查了圓周角定理,相似三角形的判定和性質,平行線的性質,勾股定理,切線的性質,等腰三角形的性質,正確的作出輔助線構造相似三角形是解題的關鍵.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
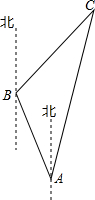 為有效開發海洋資源,保護海洋權益,我國對南海諸島進行了全面調查,一測量船在A島測得B島在北偏西30°,C島在北偏東15°,航行100海里到達B島,在B島測得C島在北偏東45°,求B,C兩島及A,C兩島的距離($\sqrt{6}$≈2.45,結果保留到整數)
為有效開發海洋資源,保護海洋權益,我國對南海諸島進行了全面調查,一測量船在A島測得B島在北偏西30°,C島在北偏東15°,航行100海里到達B島,在B島測得C島在北偏東45°,求B,C兩島及A,C兩島的距離($\sqrt{6}$≈2.45,結果保留到整數)查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com