Question

19．如圖1，將矩形OABC放置在平面直角坐標系中，且A（3，0），C（0，3$\sqrt{3}$）．拋物線y=ax²+bx過點B，且與x軸的一個交點為D（6，0）．
（1）求a，b的值．
（2）若點P是x軸上方的拋物線上一動點，連接PA，PC，當△PAC面積最大時，求點P的坐標．
（3）如圖2，若線段AB上有一動點，從點B出發，以某一速度勻速運動到某一位置Q處，然后以原來速度的2倍，沿線段QO運動到原點O處．試確定點Q的位置，使得按照上述要求到達原點所用的時間最短．

Answer 1

分析 （1）根據矩形的性質，可得B點坐標，根據待定系數法，可得函數解析式；
（2）根據平行于AC且與拋物線相切的直線到AC的距離最大，可得P是平行線與拋物線的唯一交點，根據解方程組，可得P點坐標；也可以利用面積差表示△PAC的面積，得出函數關系式，求最值，也可以求出點P的坐標；
（3）連接BD，過O作OM⊥BD于點M，交AB于點Q，接下來證明∠QBM=30°，從而可得到從點Q到A與點Q到點O所用時間相同，從而可確定出Q的坐標．

解答 解：（1）由矩形OABC放置在平面直角坐標系中，且A（3，0），C（0，3$\sqrt{3}$），得：
B點坐標為（3，3$\sqrt{3}$）．
將B、D點坐標代入函數解析式，得：
$\left\{\begin{array}{l}{9a+3b=3\sqrt{3}}\\{36a+6b=0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=-\frac{\sqrt{3}}{3}}\\{b=2\sqrt{3}}\end{array}\right.$，
（2）如圖1，過點P作平行于AC的直線，此直線與拋物線僅有一個交點時，△PAC的面積最大，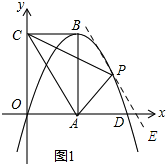
∵A（3，0），C（0，3$\sqrt{3}$），
∴直線AC的解析式為：y=-$\sqrt{3}$x+3$\sqrt{3}$，
設過點P的直線解析式為y=-$\sqrt{3}$x+b，聯立直線于拋物線解析式，得$\left\{\begin{array}{l}{y=-\sqrt{3}x+b}\\{y=-\frac{\sqrt{3}}{3}{x}^{2}+2\sqrt{3}x}\end{array}\right.$，
整理，得$\frac{\sqrt{3}}{3}$x²-3$\sqrt{3}$x+b=0，
△=81-4$\sqrt{3}$b=0，
解得b=$\frac{27}{4}\sqrt{3}$；
$\frac{\sqrt{3}}{3}$x²-3$\sqrt{3}$x+$\frac{27}{4}\sqrt{3}$=0，
解得x₁=x₂=$\frac{9}{2}$，y=-$\sqrt{3}$×$\frac{9}{2}$+$\frac{27}{4}\sqrt{3}$=$\frac{9\sqrt{3}}{4}$，
即P點坐標為（$\frac{9}{2}$，$\frac{9\sqrt{3}}{4}$）；
（3）如圖2，連接BD，過O作OM⊥BD于點M，交AB于點Q，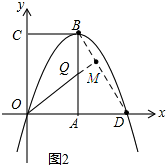
∵AD=3，AB=3$\sqrt{3}$，
∴∠QBM=30°，
又∵QM⊥BD，
∴∠QOA=30°
∴AQ=$\frac{1}{2}$OQ，
∴設動點在BQ上的速度為1，則在OQ上的速度為2，
∴動點在OQ上運動的時間等于動點以原速度在AQ上運動的時間，
即從點B運動到Q，再運動到O，相當于以原速度從B運動到A的時間，
∴當OM⊥BD時，交AB于Q，這時的點Q就是所求的點，
tan30°=$\frac{AQ}{AO}$=$\frac{\sqrt{3}}{3}$，
∴$\frac{AQ}{3}$=$\frac{\sqrt{3}}{3}$，
∴AQ=$\sqrt{3}$，
∴Q（3，$\sqrt{3}$）．

點評 本題是二次函數的綜合題，考查了利用待定系數法求函數的解析式，這是常考題型，要熟練掌握；還考查了利用最值求點的坐標，把這一問題轉化為利用方程組求交點的問題，也可以利用二次函數的頂點坐標（最值）來求點的坐標；本題把函數和幾何有機的結合在一起，看似簡單，其實比較復雜，要認真理解題意，要把時間的最小值問題轉化為線段的最小值來解決問題．