
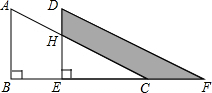
 如圖,將Rt△ABC沿射線BC方向平移得到△DEF,已知AB=16cm,BE=10cm,DH=6cm,則圖中陰影部分的面積為130cm2.
如圖,將Rt△ABC沿射線BC方向平移得到△DEF,已知AB=16cm,BE=10cm,DH=6cm,則圖中陰影部分的面積為130cm2. 分析 根據平移的性質可得DE=AB,然后求出HE,再判斷出陰影部分的面積等于四邊形ABEH的面積,最后利用梯形的面積公式列式計算即可得解.
解答 解:∵將Rt△ABC沿射線BC方向平移得到△DEF,
∴DE=AB=16cm,
∵DH=6cm,
∴HE=DE-DH=10cm,
∵∠B=90°,
∴四邊形ABEH是梯形,
S陰影=S△DEF-S△CEH=S△ABC-S△CEH=S梯形ABEH
=$\frac{1}{2}$(AB+HE)•BE
=$\frac{1}{2}$×(16+10)×10
=130(cm2).
故答案為:130cm2.
點評 本題考查平移的基本性質:①平移不改變圖形的形狀和大小;②經過平移,對應點所連的線段平行且相等,對應線段平行且相等,對應角相等;本題判斷出陰影部分的面積與四邊形的面積相等是解題的關鍵.


 小學課時作業全通練案系列答案
小學課時作業全通練案系列答案 金版課堂課時訓練系列答案
金版課堂課時訓練系列答案 單元全能練考卷系列答案
單元全能練考卷系列答案 新黃岡兵法密卷系列答案
新黃岡兵法密卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,一段拋物線:y=x(x-3)(0≤x≤3),記為C1,它與x軸交于點O,A,將C1繞點A1旋轉180°得C2,交x軸于點A2;將C2繞點A2旋轉180°得C3,交x軸于點A3;…,如此進行下去,直至得C673.若P(2017,a)在第673段拋物線C673上,則a=-2.
如圖,一段拋物線:y=x(x-3)(0≤x≤3),記為C1,它與x軸交于點O,A,將C1繞點A1旋轉180°得C2,交x軸于點A2;將C2繞點A2旋轉180°得C3,交x軸于點A3;…,如此進行下去,直至得C673.若P(2017,a)在第673段拋物線C673上,則a=-2.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com