
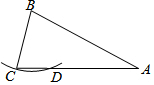
 如圖,在△ABC中,AB=AC=2BC,以點B為圓心,BC長為半徑作弧,與AC交于點D.若AC=4,則線段CD的長為1.
如圖,在△ABC中,AB=AC=2BC,以點B為圓心,BC長為半徑作弧,與AC交于點D.若AC=4,則線段CD的長為1. 分析 連結BD,然后依據等邊對等角的性質證明∠C=∠BDC,∠C=∠CBA,從而可證明△BCD∽△ACB,最后依據相似三角形的性質求解即可.
解答 解:如圖所示:連結BD.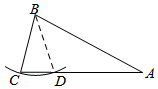
∵AB=AC=2BC,AC=4,
∴BC=2.
∵BC=BD,
∴∠C=∠BDC.
∵AB=AC,
∴∠C=∠CBA.
∴∠BDC=∠CBA.
又∵∠C=∠C,
∴△BCD∽△ACB.
∴$\frac{CD}{CB}$=$\frac{CB}{AC}$即$\frac{CD}{2}$=$\frac{2}{4}$,解得:CD=1.
故答案為:1.
點評 本題主要考查的是相似三角形的性質和判定、等腰三角形的性質,熟練掌握相關知識是解題的關鍵.


科目:初中數學 來源: 題型:填空題
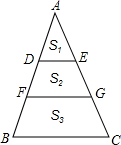 如圖,△ABC中,DE∥FG∥BC.
如圖,△ABC中,DE∥FG∥BC.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
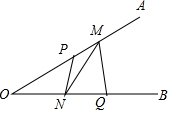 已知∠AOB=30°,點P、Q分別是邊OA、OB上的定點,OP=3,OQ=4,點M、N是分別是邊OA、OB上的動點,則折線P-N-M-Q長度的最小值是5.
已知∠AOB=30°,點P、Q分別是邊OA、OB上的定點,OP=3,OQ=4,點M、N是分別是邊OA、OB上的動點,則折線P-N-M-Q長度的最小值是5.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
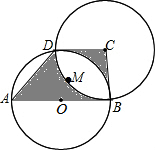 如圖,AB為圓O的直徑,點D在圓O上,在梯形ABCD中:
如圖,AB為圓O的直徑,點D在圓O上,在梯形ABCD中:查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 汽車以120Km/h的速度勻速行駛,行駛路程y(Km)與時間t(h)之間的關系 | |
| B. | 等腰三角形頂角y與底角x間的關系 | |
| C. | 高為4cm的圓錐體積y (cm3)與底面半徑x (cm)的關系 | |
| D. | 一棵樹現在高50cm,每月長高3cm,x個月后這棵樹的高度y (cm)與生長月數x(月)之間的關系 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 678.89×108元 | B. | 67.889×109元 | C. | 6.7889×109元 | D. | 6.7889×1010元 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com