Question

7．如圖，在平面直角坐標系中，過格點A、B、C作一圓弧．
（1）直接寫出該圓弧所在圓的圓心D的坐標； 
（2）求弧AC的長（結果保留π）；
（3）連接AC、BC，則sinC=$\frac{\sqrt{5}}{5}$．

Answer 1

分析 （1）根據垂徑定理的推論：弦的垂直平分線必過圓心，可以作弦AB和BC的垂直平分線，交點即為圓心，寫出圓心坐標即可；
（2）根據正方形的性質和勾股定理以及弧長公式計算即可；
（3）根據正弦的定義計算即可．

解答 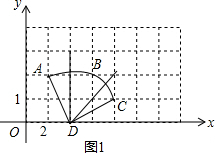解：（1）根據垂徑定理的推論：弦的垂直平分線必過圓心，
作弦AB和BC的垂直平分線，交點D即為圓心．
如圖1所示，則圓心D的坐標是（2，0）；
（2）由圖1可知，∠ADC=90°，AD=$\sqrt{5}$，
∴弧AC的長為：$\frac{90π×\sqrt{5}}{180}$=$\frac{\sqrt{5}}{2}$π；
（3）如圖2，由勾股定理得AE=$\sqrt{2}$，AC=$\sqrt{10}$，
由正方形的性質和格點的性質可知，∠AEC=90°，
則sinC=$\frac{AE}{AC}$=$\frac{\sqrt{2}}{\sqrt{10}}$=$\frac{\sqrt{5}}{5}$，
故答案為：$\frac{\sqrt{5}}{5}$．

點評 本題考查的是垂徑定理、勾股定理、弧長的計算，掌握弦的垂直平分線經過圓心、弧長的計算公式是解題的關鍵．