
(12分)如圖1,將兩個完全相同的三角形紙片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作發現
如圖2,固定△ABC,使△DEC繞點C旋轉,當點D恰好落在AB邊上時,填空:
①線段DE與AC的位置關系是_________;(2分)
②設△BDC的面積為S1,△AEC的面積為S2,則S1與S2的數量關系是_________________.(2分)

(2)猜想論證
當△DEC繞點C旋轉到圖3所示的位置時,小明猜想(1)中S1與S2的數量關系仍然成立,并嘗試分別作出了△BDC和△AEC中BC、CE邊上的高,請你證明小明的猜想.(5分)
(3)拓展探究
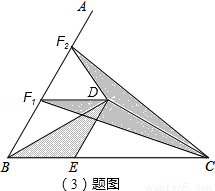
已知∠ABC=60°,點D是其角平分線上一點,BD=CD=4,DE//AB交BC于點E(如圖4).
若在射線BA上存在點F,使 ,請直接寫出相應的BF的長:BF=_____.(3分)
,請直接寫出相應的BF的長:BF=_____.(3分)

(1)①DE∥AC;②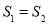 ;(2)成立,證明見試題解析;(3)
;(2)成立,證明見試題解析;(3)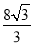 或
或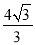 .
.
【解析】
試題分析:(1)①根據旋轉的性質可得AC=CD,然后求出△ACD是等邊三角形,根據等邊三角形的性質可得∠ACD=60°,然后根據內錯角相等,兩直線平行解答;
②根據等邊三角形的性質可得AC=AD,再根據直角三角形30°角所對的直角邊等于斜邊的一半求出AC=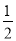 AB,然后求出AC=BD,再根據等邊三角形的性質求出點C到AB的距離等于點D到AC的距離,然后根據等底等高的三角形的面積相等解答;
AB,然后求出AC=BD,再根據等邊三角形的性質求出點C到AB的距離等于點D到AC的距離,然后根據等底等高的三角形的面積相等解答;
(2)根據旋轉的性質可得BC=CE,AC=CD,再求出∠ACN=∠DCM,然后利用“角角邊”證明△ACN和△DCM全等,根據全等三角形對應邊相等可得AN=DM,然后利用等底等高的三角形的面積相等證明;
(3)過點D作DF1∥BE,求出四邊形BEDF1是菱形,根據菱形的對邊相等可得BE=DF1,然后根據等底等高的三角形的面積相等可知點F1為所求的點,過點D作DF2⊥BD,求出∠F1DF2=60°,從而得到△DF1F2是等邊三角形,然后求出DF1=DF2,再求出∠CDF1=∠CDF2,利用“邊角邊”證明△CDF1和△CDF2全等,根據全等三角形的面積相等可得點F2也是所求的點,然后在等腰△BDE中求出BE的長,即可得解.
試題解析:(1)①∵△DEC繞點C旋轉點D恰好落在AB邊上,∴AC=CD,
∵∠BAC=90°﹣∠B=90°﹣30°=60°,∴△ACD是等邊三角形,∴∠ACD=60°,
又∵∠CDE=∠BAC=60°,∴∠ACD=∠CDE,∴DE∥AC;
②∵∠B=30°,∠C=90°,∴CD=AC=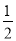 AB,∴BD=AD=AC,
AB,∴BD=AD=AC,
根據等邊三角形的性質,△ACD的邊AC、AD上的高相等,
∴△BDC的面積和△AEC的面積相等(等底等高的三角形的面積相等),即S1=S2;
故答案為:DE∥AC;S1=S2;
(2)如圖,∵△DEC是由△ABC繞點C旋轉得到,∴BC=CE,AC=CD,
∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°﹣90°=90°,∴∠ACN=∠DCM,
在△ACN和△DCM中,∵∠ACN=∠DCM,∠CMD=∠N=90°,AC=CD,∴△ACN≌△DCM(AAS),
∴AN=DM,∴△BDC的面積和△AEC的面積相等(等底等高的三角形的面積相等),即S1=S2;
(3)如圖,過點D作DF1∥BE,易求四邊形BEDF1是菱形,所以BE=DF1,且BE、DF1上的高相等,
此時S△DCF1=S△BDE;過點D作DF2⊥BD,∵∠ABC=60°,F1D∥BE,∴∠F2F1D=∠ABC=60°,
∵BF1=DF1,∠F1BD=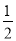 ∠ABC=30°,∠F2DB=90°,∴∠F1DF2=∠ABC=60°,
∠ABC=30°,∠F2DB=90°,∴∠F1DF2=∠ABC=60°,
∴△DF1F2是等邊三角形,∴DF1=DF2,
∵BD=CD,∠ABC=60°,點D是角平分線上一點,∴∠DBC=∠DCB=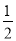 ×60°=30°,
×60°=30°,
∴∠CDF1=180°﹣∠BCD=180°﹣30°=150°,∠CDF2=360°﹣150°﹣60°=150°,∴∠CDF1=∠CDF2,在△CDF1和△CDF2中,∵ DF1=DF2,∠CDF1=∠CDF2,CD=CD,
∴△CDF1≌△CDF2(SAS),∴點F2也是所求的點,
∵∠ABC=60°,點D是角平分線上一點,DE∥AB,∴∠DBC=∠BDE=∠ABD=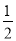 ×60°=30°,
×60°=30°,
又∵BD=4,∴BE=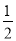 ×4÷cos30°=
×4÷cos30°=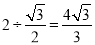 ,∴BF1=
,∴BF1=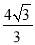 ,BF2=BF1+F1F2=
,BF2=BF1+F1F2=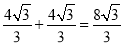 ,
,
故BF的長為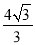 或
或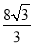 .
.
考點:全等三角形的判定與性質.


科目:初中數學 來源:2014-2015學年福建泉州惠安第三教區八年級上學期期中數學試卷(解析版) 題型:解答題
(9分)如圖,A、D、F、B在同一直線上,AF=BD,AE=BC,且AE∥BC.

求證:(1)△AEF≌△BCD.
(2)∠C=∠E
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省南平市八年級上學期期中考試數學試卷(解析版) 題型:填空題
如圖,在△ABC中,∠C=90°,AD平分∠CAB,BC=8cm,BD=5cm,那么D點到直線AB的距離是 _________ cm.

查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省、三中、城關小學九年級上學期期中聯考數學試卷(解析版) 題型:選擇題
若一元二次方程式 的兩根為
的兩根為 ,其中a、b為兩數,則
,其中a、b為兩數,則 之值為( )
之值為( )
A. B.
B. C.3 D.5
C.3 D.5
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省泉州市惠安第三教研片區九年級上學期期中考試數學試卷(解析版) 題型:選擇題
下列各組中的四條線段是成比例線段的是( )
A.a=6,b=4,c=10,d=5 B.a=3,b=7,c=2,d= 9
C.a=2,b=4,c=3,d=6 D.a=4,b=11,c=3,d=2
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省、三中、城關小學九年級上學期期中聯考數學試卷(解析版) 題型:解答題
(8分)如圖,△AOB中,OA=OB,以O為圓心的圓經過AB上兩點C、D,則AC與BD相等嗎?請說明理由.

查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省泉州市惠安第三教研片區九年級上學期期中考試數學試卷(解析版) 題型:解答題
(9分)如圖,在梯形ABCD中,AD∥BC,∠B=∠ACD.

(1)證明:△ABC∽△DCA;
(2)若AC=6,BC=9,求AD長.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省九年級上學期期中質量監測數學試卷(解析版) 題型:解答題
(7分)已知:關于x的方程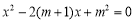
(1)當m取什么值時,原方程沒有實數根;
(2)對m選取一個你喜歡的非零整數,使原方程有兩個實數根,并求這兩個實數根的平方和.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com