
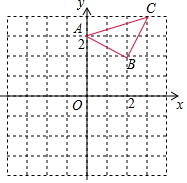
 如圖,在平面直角坐標系內(nèi),△ABC三個頂點坐標分別為A(0,3)、B(2,2)、C(3,4).
如圖,在平面直角坐標系內(nèi),△ABC三個頂點坐標分別為A(0,3)、B(2,2)、C(3,4).分析 (1)(2)畫出符合條件的三角形,如圖所示,并寫出點的坐標;
(2)B經(jīng)過的路徑總長=BB1+90°的圓心角對應的弧長.
解答  解:(1)畫出的△A1B1C1如圖所示,點點C1的坐標(3,2),
解:(1)畫出的△A1B1C1如圖所示,點點C1的坐標(3,2),
故答案為:(3,2);
(2)畫出的△A2B2C2如圖所示,點點C2的坐標(1,-2),
故答案為:(1,-2);
(3)由圖形得:第一次向下平移點B經(jīng)過的路徑為:BB1=2,
由勾股定理得:A1B2=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
第二次繞著點A1順時針旋轉(zhuǎn)90°時點B經(jīng)過的路徑為:
l=$\frac{90π×\sqrt{5}}{180}$=$\frac{\sqrt{5}}{2}$π,
∴總路徑為:2+$\frac{\sqrt{5}}{2}$π.
點評 本題考查了平移變換和旋轉(zhuǎn)變換,根據(jù)旋轉(zhuǎn)的性質(zhì)可知,通過作相等的角,在角的邊上截取相等的線段的方法,找到對應點,順次連接得出旋轉(zhuǎn)后的圖形.


科目:初中數(shù)學 來源: 題型:解答題
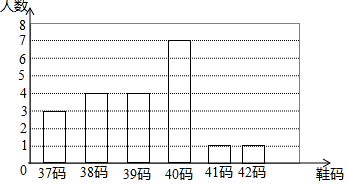 某鞋廠為了了解初中學生穿鞋的鞋號情況,對某中學八年級(1)班的20名男生所穿鞋號進行了調(diào)查,結(jié)果如圖所示
某鞋廠為了了解初中學生穿鞋的鞋號情況,對某中學八年級(1)班的20名男生所穿鞋號進行了調(diào)查,結(jié)果如圖所示查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖,已知二次函數(shù)y=-x2+bx+c的圖象過點A(3,0),B(0,3)
如圖,已知二次函數(shù)y=-x2+bx+c的圖象過點A(3,0),B(0,3)查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3,點D是BC邊上一動點(不與點B、C重合),過點D作DE⊥BC交AB邊于點E,將∠B沿直線DE翻折,點B落在射線BC上的點F處,當△AEF為直角三角形時,求BD的長.
如圖,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3,點D是BC邊上一動點(不與點B、C重合),過點D作DE⊥BC交AB邊于點E,將∠B沿直線DE翻折,點B落在射線BC上的點F處,當△AEF為直角三角形時,求BD的長.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖,若點A在數(shù)軸上對應的數(shù)為a,點B在數(shù)軸上對應的數(shù)為b,且a,b滿足|a+2|+(b-1)2=0.點A與點B之間的距離表示為AB(以下類同).
如圖,若點A在數(shù)軸上對應的數(shù)為a,點B在數(shù)軸上對應的數(shù)為b,且a,b滿足|a+2|+(b-1)2=0.點A與點B之間的距離表示為AB(以下類同).查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | ma+1=mb+1 | B. | ma-3=mb-3 | C. | a=b | D. | -2ma-1=-2mb-1 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com