
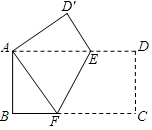
 如圖,把一張長為8cm,寬為4cm 的長方形紙片折疊,折疊后使相對的兩個點A、C重合,點D落在D′,折痕為EF.
如圖,把一張長為8cm,寬為4cm 的長方形紙片折疊,折疊后使相對的兩個點A、C重合,點D落在D′,折痕為EF.分析 (1)由矩形的性質得出AD∥BC,由平行線的性質得出∠AEF=∠CFE,由折疊的性質得出∠AFE=∠CFE,AF=CF,求出∠AEF=∠AFE,得出AE=AF即可;
(2)設AE=AF=CF=x,則BF=BC-CF=8-x,在Rt△ABF中,由勾股定理得出方程,解方程求出AE=5cm,求出△AEF的面積即可.
解答 (1)證明:∵四邊形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠AEF=∠CFE,
由折疊的性質得:∠AFE=∠CFE,AF=CF,
∴∠AEF=∠AFE,
∴AE=AF,
即△AEF是等腰三角形;
(2)解:∵AE=AF,AF=CF,
∴AE=AF=CF,
設AE=AF=CF=x,則BF=BC-CF=8-x,
在Rt△ABF中,由勾股定理得:AB2+BF2=AF2,
即42+(8-x)2=x2,
解得:x=5,
∴AE=5cm,
∴△AEF的面積=$\frac{1}{2}$×5×4=10(cm2),
即重合部分的面積為10cm2.
點評 本題考查了矩形的性質、折疊的性質、等腰三角形的判定、勾股定理以及三角形面積的計算;熟練掌握矩形的性質和折疊的性質,由勾股定理得出方程是解決問題(2)的關鍵.


科目:初中數學 來源: 題型:解答題
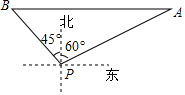 如圖,一艘輪船位于燈塔P北偏東60°方向上,距離燈塔40海里的A處,它向西航行多少海里到達燈塔P北偏西45°方向上的B處.(參考數據:$\sqrt{3}$≈1.732,結果精確到0.1)
如圖,一艘輪船位于燈塔P北偏東60°方向上,距離燈塔40海里的A處,它向西航行多少海里到達燈塔P北偏西45°方向上的B處.(參考數據:$\sqrt{3}$≈1.732,結果精確到0.1)查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,?ABCD中,兩個全等的等腰直角三角形的面積都為S1,兩個全等的直角三角形的面積均為S2,中間的是面積為S3正方形.求證:2S2+S3=2S1.
如圖,?ABCD中,兩個全等的等腰直角三角形的面積都為S1,兩個全等的直角三角形的面積均為S2,中間的是面積為S3正方形.求證:2S2+S3=2S1.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com