
分析 (1)把P、Q的坐標代入反比例函數解析式可求得m、n的值,再把P、Q坐標代入直線解析式可求得k、b的值;
(2)結合(1)可先求得A、B坐標,可求得C點坐標,再由條件可求得直線OD的解析式,由BO=CD可求得D點坐標.
解答 解:
(1)把P(1,m)代入y=$\frac{5}{x}$,得 m=5,
∴P(1,5),
把Q(n,1)代入y=$\frac{5}{x}$,得 n=5,
∴Q(5,1),
P(1,5)、Q(5,1)代入y=kx+b得 $\left\{{\begin{array}{l}{k+b=5}\\{5k+b=1}\end{array}}\right.$,解得$\left\{{\begin{array}{l}{k=-1}\\{b=6}\end{array}}\right.$,
即k=-1,b=6;
(2)由(1)知 y=-x+6,
∴A(6,0)B(0,6)
∵C點在直線AB上,
∴設C(x,-x+6),
由AB=AC得$\sqrt{{6}^{2}+{6}^{2}}$=$\sqrt{(x-6)^{2}+(-x+6)^{2}}$,
解得x=12或x=0(不合題意,舍去),
∴C(12,-6),
∵直線OD∥BC 且過原點,
∴直線OD解析式為y=-x,
∴可設D(a,-a),
由OB=CD 得6=$\sqrt{(a-12)^{2}+(-a+6)^{2}}$,
解得a=12或a=6,
∴滿足條件的點D坐標是(12,-12)或(6,-6).
點評 本題主要考查函數圖象的交點,掌握函數圖象的交點坐標滿足每一個函數解析式是解題的關鍵,在(2)中注意直線PD的位置.


 導學與測試系列答案
導學與測試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:初中數學 來源: 題型:解答題
 在平面直角坐標系中,△ABO的三個頂點坐標分別為:A(2,3)、B(3,1)、O(0,0).
在平面直角坐標系中,△ABO的三個頂點坐標分別為:A(2,3)、B(3,1)、O(0,0).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
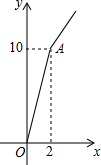 某玉米種子的價格為a元/千克,如果一次購買2千克以上的種子,超過2千克部分的種子價格打8折,小剛同學對購買量和付款金額這兩個變量的對應關系用列表法做了分析,并繪制出了函數圖象,以下是小剛繪制的表格和圖象的不完整資料,已知點A的坐標為(2,10),請你結合表格和圖象解答下列問題:
某玉米種子的價格為a元/千克,如果一次購買2千克以上的種子,超過2千克部分的種子價格打8折,小剛同學對購買量和付款金額這兩個變量的對應關系用列表法做了分析,并繪制出了函數圖象,以下是小剛繪制的表格和圖象的不完整資料,已知點A的坐標為(2,10),請你結合表格和圖象解答下列問題:| 付款金額 | a | 7.5 | 10 | 12 | b |
| 購買量(千克) | 1 | 1.5 | 2 | 2.5 | 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,將方格紙中的三角形ABC先向右平移2格得到三角形DEF,再將三角形DEF向上平移3格得到三角形GPH,
如圖,將方格紙中的三角形ABC先向右平移2格得到三角形DEF,再將三角形DEF向上平移3格得到三角形GPH,查看答案和解析>>
科目:初中數學 來源: 題型:解答題
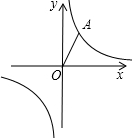 在平面直角坐標系中,已知反比例函數y=$\frac{k}{x}$的圖象經過點A,點O是坐標原點,OA=2且OA與x軸的夾角是60°.
在平面直角坐標系中,已知反比例函數y=$\frac{k}{x}$的圖象經過點A,點O是坐標原點,OA=2且OA與x軸的夾角是60°.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com