
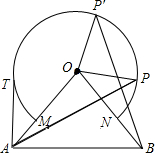
 如圖,△OAB中,OA=OB=10,∠AOB=70°,以點O為圓心,6為半徑的優弧$\widehat{MN}$分別交OA、OB于點M,N.
如圖,△OAB中,OA=OB=10,∠AOB=70°,以點O為圓心,6為半徑的優弧$\widehat{MN}$分別交OA、OB于點M,N.分析 (1)首先根據已知得出∠AOP=∠BOP′,進而得出△AOP≌△BOP′,即可得出答案;
(2)利用切線的性質得出∠ATO=90°,再利用勾股定理求出AT的長,進而得出TH的長即可得出答案;
(3)當OQ⊥OA時,△AOQ面積最大,且左右兩半弧上各存在一點分別求出即可.
解答 (1)證明:如圖1,∵∠AOP=∠AOB+∠BOP=80°+∠BOP,
∠BOP′=∠POP′+∠BOP=80°+∠BOP,
∴∠AOP=∠BOP′,
∵在△AOP和△BOP′中
$\left\{\begin{array}{l}{OA=OB}\\{∠AOP=∠BOP′}\\{OP=OP′}\end{array}\right.$,
∴△AOP≌△BOP′(SAS),
∴AP=BP′;
(2)解:如圖1,連接OT,過點T作TH⊥OA于點H,
∵AT是⊙O的切線,
∴∠ATO=90°,
∴AT=$\sqrt{O{A}^{2}-O{T}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∵$\frac{1}{2}$×OA×TH=$\frac{1}{2}$×AT×OT,
即$\frac{1}{2}$×10×TH=$\frac{1}{2}$×8×6,
解得:TH=$\frac{24}{5}$,即點T到OA的距離為$\frac{24}{5}$;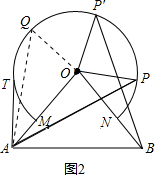
(3)解:如圖2,當OQ⊥OA時,△AOQ的面積最大;
理由:∵OQ⊥OA,
∴QO是△AOQ中最長的高,則△AOQ的面積最大,
∴∠BOQ=∠AOQ+∠AOB=90°+70°=160°,
當Q點在優弧$\widehat{MN}$右側上,
∵OQ⊥OA,
∴QO是△AOQ中最長的高,則△AOQ的面積最大,
∴∠BOQ=∠AOQ-∠AOB=90°-70°=20°,
綜上所述:當∠BOQ的度數為20°或160°時,△AOQ的面積最大.
點評 本題考查了圓的綜合題、切線的判定與性質、全等三角形的判定與性質,第二個問題的關鍵是利用面積法求出線段TH,第三個問題的關鍵是學會用分類討論的思想思考問題,注意一題多解,屬于中考壓軸題.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,設四邊形ABCD是邊長為1的正方形,以對角線AC為邊作第2個正方形ACEF,再以對角線AE為邊作第3個正方形AEGH,如此下去…,記正方形ABCD的面積S1=1,按上述方法所作的正方形的面積依次為S2,S3…,Sn,則Sn=( )
如圖,設四邊形ABCD是邊長為1的正方形,以對角線AC為邊作第2個正方形ACEF,再以對角線AE為邊作第3個正方形AEGH,如此下去…,記正方形ABCD的面積S1=1,按上述方法所作的正方形的面積依次為S2,S3…,Sn,則Sn=( )| A. | 2n-1 | B. | 2n | C. | 2n+1 | D. | 2n+2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com