Question

14．已知A（0，a），B（b，0），且a，b滿足（2a-1）²+|b-$\frac{1}{2}$|=0．

（1）求△AOB的面積；
（2）如圖，點C在線段AB上（A．B兩端點除外），AD⊥AB，且∠DOC=45°，求證：OD平分∠ADC；
（3）若C是射線BA上一動點（點C為AB的中點除外，且點C不與A點重合），連CO，將OC繞C順時針方向旋轉90°到CD，連AD，求∠CAD的度數．

Answer 1

分析 （1）根據非負數的性質得到2a-1=0，b-$\frac{1}{2}$=0，求得a=$\frac{1}{2}$，b=$\frac{1}{2}$，得到OA=OB=$\frac{1}{2}$，根據三角形的面積公式即可得到結果；
（2）延長DA到E，使AE=BC，根據AD⊥AB，求得∠OAE=45°=∠OBC，推出△OAE≌△OBC，根據全等三角形的性質得到OE=OC，∠EOA=∠COB，由∠DOC=45°，于是得到∠DOE=∠EOA+∠AOD=∠COB+∠AOD=90°-∠DOC=45°，推出△ODE≌△ODC，根據全等三角形的性質即可得到結論；
（3）①如圖2：當C點在線段AB外，過O作OE⊥AB于E，過D作DF⊥AB于F，根據等腰直角三角形的性質得到OE=AE，通過△CDF≌△COE，得到DF=CE，CF=OE證得△ADF是等腰直角三角形，于是得到結論；②當C點在線段AB內，如圖3所示，過O作OE⊥AB于E，過D作DF⊥AB于F，根據等腰直角三角形的性質得到OE=AE，通過△CDF≌△COE，得到DF=CE，CF=OE證得△ADF是等腰直角三角形，于是得到結論．

解答 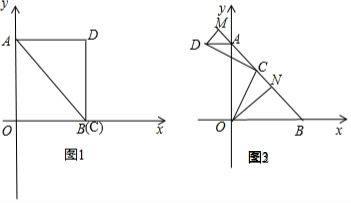解：（1）∵a，b滿足（2a-1）²+|b-$\frac{1}{2}$|=0，
∴2a-1=0，b-$\frac{1}{2}$=0，
∴a=$\frac{1}{2}$，b=$\frac{1}{2}$，
∴OA=OB=$\frac{1}{2}$，
∴S_△AOB=$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}$=$\frac{1}{8}$；
（2）∵OA=OB，
∴∠OAB=∠OBA=45°，
如圖1，延長DA到E，使AE=BC，連接OE，
∵AD⊥AB，∴∠OAE=45°=∠OBC，
在△OAE與△OBC中，$\left\{\begin{array}{l}{AE=BC}\\{∠EAO=∠OBC}\\{AO=BO}\end{array}\right.$，
∴△OAE≌△OBC，
∴OE=OC，∠EOA=∠COB，
∵∠DOC=45°，
∴∠DOE=∠EOA+∠AOD=∠COB+∠AOD=9°-∠DOC=45°，
在△ODE與△ODC中，$\left\{\begin{array}{l}{OE=OC}\\{∠DOE=∠DOC}\\{OD=DO}\end{array}\right.$，
∴△ODE≌△ODC，
∴∠ODE=∠ODC，
即OD平分∠ADC；

（3）①如圖1，當點C與點B重合時，
∵△AOB是等腰直角三角形，
∴OA=OB，∠OAB=45°，
∵OC=CD，∴OD=CD，
∴四邊形ADOC是正方形，
∴∠OAD=90°，
∴∠CAD=∠AOD-∠OAB=45°；
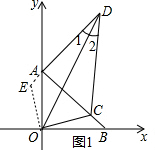
②如圖2，當C在AB中點與B相連的線段上時，過D作DM⊥AB，ON⊥AB，
∴∠CMD=∠ONC=90°，
∵∠DCO=90°，
∴∠DCM+∠OCM=90°，
∴∠DCM=∠OCN，
在△DCM與△OCN中，$\left\{\begin{array}{l}{∠CMD=∠ONC}\\{∠DCM=∠OCN}\\{CD=CO}\end{array}\right.$，
∴△DCM≌△OCN，
∵△AOB是等腰直角三角形，
∴∠OAB=45°，
∴∠MOA=45°，
∴NA=NO，
∴AN=MC，
∴AM=NC，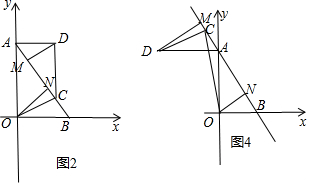
∴AM=MD，
∴∠CAD=$\frac{180°-90°}{2}$=45°；
③如圖3，當C在AB是中點與A之間時，同理AM=MD，∴∠MAD=45°，
∴∠DAC=180°-∠MAD=135°；
④如圖4，當C在BA的延長線上時，同理可得AM=MD，
∴∠DAC=45°，
綜上所述，∠CAD的度數為45°或135°．

點評 本題考查了全等三角形的判定和性質，坐標與圖形的性質，等腰直角三角形的性質，旋轉的性質，正確的作出輔助線構造全等三角形是解題的關鍵．