
分析 (1)根據題意分別得出y1、y2與x之間的函數關系式;
(2)根據題意得出y與x的關系式,進而利用二次函數增減性得出答案.
解答 解:(1)由題意可得:y1=180+x,y2=$\frac{1}{2}$x;
(2)由題意可得:y=(180+x)(160-$\frac{1}{2}$x),
即:y=-$\frac{1}{2}$(x-70)2+31250,
當x=70時,可獲最大日租金收入31250元,因為31250>160×180,
又因為每次提價為20元,
所以x是不可能取到70,
根據二次函數的對稱性,與70最接近的兩個數,都能使日租金獲得最大化,而與70最接近的兩個數分別是60或80,為了使投資少而利潤大,每輛車日租金應提高80元.
點評 此題主要考查了二次函數增減性以及二次函數的應用,正確得出y與x的函數關系式是解題關鍵.


科目:初中數學 來源: 題型:選擇題
| A. | (2x+1)(2x-1)=4x2-1 | B. | 2x3-4x2=x2(2x-4) | C. | x2-4x+4=x(x-4)+4 | D. | x2+2x+1=(x+1)2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2,3,4 | B. | 0.3,0.4,0.5 | C. | 7,24,25 | D. | $\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知二次函數y=x2-2x-3.
已知二次函數y=x2-2x-3.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
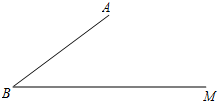 如圖,已知cos∠ABM=$\frac{4}{5}$,AB=20,C是射線BM上一點.
如圖,已知cos∠ABM=$\frac{4}{5}$,AB=20,C是射線BM上一點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com