
分析 (1)先計算出自變量為0時的函數值得到C(0,8),再通過解方程x2-6x+8=0得到A、B點的坐標,接著利用勾股定理分別計算出AB、BC、AC,然后計算出△ABC的周長$\sqrt{5}$;
(2)利用三角形面積公式計算△ABC的面積.
解答 解:(1)當x=0時,y=x2-6x+8=8,則C(0,8);
當y=0時,x2-6x+8=0,解得x1=2,x2=4,則A、B點的坐標為(2,0),(4,0),
所以AB=2,AC=$\sqrt{{2}^{2}+{8}^{2}}$=2$\sqrt{17}$,BC=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$,
所以△ABC的周長=2+2$\sqrt{17}$+4$\sqrt{5}$;
(2)△ABC的面積=$\frac{1}{2}$×8×2=8.
點評 本題考查了拋物線與x軸的交點:把求二次函數y=ax2+bx+c(a,b,c是常數,a≠0)與x軸的交點坐標問題轉化為解關于x的一元二次方程.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
 如圖,OB是∠AOC的平分線,OD是∠COE的平分線,如果∠AOB=40°,∠COE=60°,則∠BOD的度數為( )
如圖,OB是∠AOC的平分線,OD是∠COE的平分線,如果∠AOB=40°,∠COE=60°,則∠BOD的度數為( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 注入的時間(min) | 1 | 2 | 3 | 4 | 5 | 6 |
| 注入油量q(L) | 1.5 | 3 | 4.5 | 6 | 7.5 | 9 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 二次函數的圖象與x軸的交點位于y軸的兩側 | |
| B. | 二次函數的圖象與x軸的交點位于y軸的右側 | |
| C. | 其中二次函數中的c>1 | |
| D. | 二次函數的圖象與x軸的一個交于位于x=2的右側 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
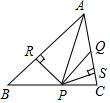 如圖,已知△ABC中,AQ=PQ、PR=PS、PR⊥AB于R,PS⊥AC于S,有以下三個結論:①AS=AR;②QP∥AR;③△BRP≌△CSP,其中( )
如圖,已知△ABC中,AQ=PQ、PR=PS、PR⊥AB于R,PS⊥AC于S,有以下三個結論:①AS=AR;②QP∥AR;③△BRP≌△CSP,其中( )| A. | 全部正確 | B. | 僅①正確 | C. | 僅①、②正確 | D. | 僅①、③正確 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | AC=BC | B. | AB=2AC | C. | AC+BC=AB | D. | $BC=\frac{1}{2}AB$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com