
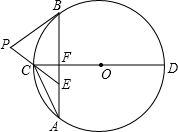
 如圖,已知⊙O的弦AB垂直于直徑CD,垂足為F,點E在AB上,且EA=EC,延長EC到點P,使PE=PB,連接AC,有下列四個結(jié)論:
如圖,已知⊙O的弦AB垂直于直徑CD,垂足為F,點E在AB上,且EA=EC,延長EC到點P,使PE=PB,連接AC,有下列四個結(jié)論:分析 ①正確.根據(jù)垂徑定理即可判斷.
②錯誤.根據(jù)已知條件不能推出CF=OF.
③正確.只要證明△CAE∽△BAC,推出$\frac{AC}{AE}$=$\frac{AB}{AC}$,即可證明.
④正確.只要證明∠OBP=90°即可.
解答 解:連接BC,OB,OA,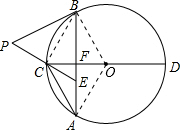
∵AB⊥CD,CD是圓的直徑,
∴BC=AC,弧AC=弧BC,故①正確;
∴∠CAB=∠CBA,
∵CE=AE,
∴∠CAB=∠ACE=∠CBA,
∵∠CAB=∠CAB,
∴△CAE∽△BAC,
∴$\frac{AC}{AE}$=$\frac{AB}{AC}$,
∴AC2=AE•AB,故③正確;
∵PB=PE,
∴∠PBA=∠PEB,
∵∠PEB=∠CAB+∠ECA=2∠CAB=2∠CBF,
∴∠PBC=∠CBE,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OBC+∠CBP=∠OCB+∠CBA=90°,
即OB⊥PB,
∵OB是圓O的半徑,
∴PB是圓O的切線,故④正確;
根據(jù)已知條件不能推出CF=OF,故②錯誤;
故答案為:①③④.
點評 本題綜合考查了等腰三角形的性質(zhì),勾股定理,相似三角形的性質(zhì)和判定,垂徑定理,含30度角的直角三角形性質(zhì),切線的判定等知識點,此題綜合性比較強,有一定的難度,對學(xué)生有較高的要求,但題型較好.


科目:初中數(shù)學(xué) 來源: 題型:解答題
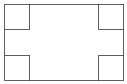 如圖所示,在長和寬分別是a、b的矩形紙片的四個角上都剪去一個邊長為x的小正方形,折成一個無蓋的紙盒.
如圖所示,在長和寬分別是a、b的矩形紙片的四個角上都剪去一個邊長為x的小正方形,折成一個無蓋的紙盒.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
 “折竹抵地”問題源自《九章算術(shù)》中,即:今有竹高一丈,末折抵地,去本四尺,問折者高幾何?意思是:一根竹子,原高一丈,一陣風將竹子折斷,其竹梢恰好抵地,抵地處離竹子底部4尺遠,則折斷后的竹子高度為4.2尺.
“折竹抵地”問題源自《九章算術(shù)》中,即:今有竹高一丈,末折抵地,去本四尺,問折者高幾何?意思是:一根竹子,原高一丈,一陣風將竹子折斷,其竹梢恰好抵地,抵地處離竹子底部4尺遠,則折斷后的竹子高度為4.2尺.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2-(-1)3=2-1=1 | B. | 74-4÷70=70÷70=1 | ||
| C. | $6÷({\frac{1}{3}-\frac{1}{2}})=6×3-6×2=6$ | D. | 23-32=8-9=1 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,已知點A,B.
如圖,已知點A,B.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{5}{2}<r<4$ | B. | $\frac{5}{2}<r<3$ | C. | 3<r<4 | D. | r>3 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
 如圖,已知A1(1,0)、A2(1,1)、A3(-1,1)、A4(-1,-1)、A5(2,-1)、…,則點A2016的坐標為(-504,-504).
如圖,已知A1(1,0)、A2(1,1)、A3(-1,1)、A4(-1,-1)、A5(2,-1)、…,則點A2016的坐標為(-504,-504).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
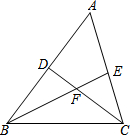 如圖,在△ABC中,∠B、∠C的平分線BE,CD相交于點F,∠A=60°,則∠BFC=( )
如圖,在△ABC中,∠B、∠C的平分線BE,CD相交于點F,∠A=60°,則∠BFC=( )| A. | 118° | B. | 119° | C. | 120° | D. | 121° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
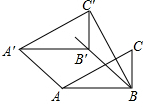 如圖,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,將Rt△ABC沿∠ABC的平分線BB′方向平移得到△A′B′C′,連結(jié)AA′,BC′.若BB′=4$\sqrt{2}$,則BC′的長為( )
如圖,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,將Rt△ABC沿∠ABC的平分線BB′方向平移得到△A′B′C′,連結(jié)AA′,BC′.若BB′=4$\sqrt{2}$,則BC′的長為( )| A. | 6 | B. | 5 | C. | 4$\sqrt{2}$+1 | D. | $\sqrt{41}$ |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com