
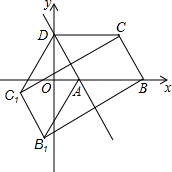
 如圖,已知?ABCD的三個頂點A(n,0),B(m,0),D(0,2n)(m>n>0),作?ABCD關于直線AD的對稱圖形AB1C1D.
如圖,已知?ABCD的三個頂點A(n,0),B(m,0),D(0,2n)(m>n>0),作?ABCD關于直線AD的對稱圖形AB1C1D.分析 (1)①先根據勾股定理,Rt△AOD中,求得AD=$\sqrt{A{O}^{2}+D{O}^{2}}$=$\sqrt{5{n}^{2}}$=$\sqrt{5}$n,再根據A(n,0),B(m,0),得出AB=m-n,最后根據AD=AB,得到$\sqrt{5}$n=m-n,進而得出$\frac{m}{n}$的值;
②設CC1與AD交于點E,根據平行線的性質,得出∠CDE=∠DAO,再根據軸對稱的性質得出,∠CED=90°=∠DOA,CE=C1E,再判定△CDE≌△DAO(AAS),即可得出CE=DO=2n,進而得到CC1=4n;
(2)根據四邊形BCEF、四邊形B1C1EF都是平行四邊形,易證S?BCEF=S?BCDA=S?B1C1DA=S?B1C1EF,從而可得S?BCC1B1=2S?BCDA=-4(n-$\frac{3}{2}$)2+9,根據二次函數的性質就可求得四邊形CC1B1B面積S的最大值.
解答 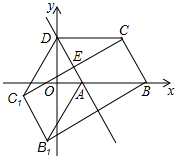 解:(1)①∵A(n,0),D(0,2n),
解:(1)①∵A(n,0),D(0,2n),
∴AO=n,DO=2n,
∴Rt△AOD中,AD=$\sqrt{A{O}^{2}+D{O}^{2}}$=$\sqrt{5{n}^{2}}$=$\sqrt{5}$n,
∵A(n,0),B(m,0),
∴AB=m-n,
當?ABCD是菱形時,AD=AB,
∴$\sqrt{5}$n=m-n,即($\sqrt{5}$+1)n=m,
∴$\frac{m}{n}$=$\sqrt{5}$+1;
②設CC1與AD交于點E,
∵CD∥x軸,
∴∠CDE=∠DAO,
∵點C與點C1關于直線AD對稱,
∴AD垂直平分CC1,
∴∠CED=90°=∠DOA,CE=C1E,
∵四邊形ABCD是菱形,
∴CD=DA,
在△CDE和△DAO中,
$\left\{\begin{array}{l}{∠CED=∠DOA}\\{∠CDE=∠DAO}\\{CD=DA}\end{array}\right.$,
∴△CDE≌△DAO(AAS),
∴CE=DO=2n,
∴C1E=2n,
∴CC1=2n+2n=4n;
(2)∵?ABCD與四邊形AB1C1D關于直線AD對稱,
∴四邊形AB1C1D是平行四邊形,CC1⊥EF,BB1⊥EF,
∴BC∥AD∥B1C1,CC1∥BB1,
∴四邊形BCEF、四邊形B1C1EF都是平行四邊形,
∴S?BCEF=S?BCDA=S?B1C1DA=S?B1C1EF,
∴S?BCC1B1=2S?BCDA,
∵A(n,0),B(m,0),D(0,2n),m=3,
∴AB=m-n=3-n,OD=2n,
∴S?BCDA=AB•OD=(3-n)•2n=-2(n2-3n)=-2(n-$\frac{3}{2}$)2+$\frac{9}{2}$,
∴S?BCC1B1=2S?BCDA=-4(n-$\frac{3}{2}$)2+9,
∵-4<0,
∴當n=$\frac{3}{2}$時,S?BCC1B1最大值為9.
點評 本題屬于四邊形綜合題,主要考查了菱形的性質,軸對稱的性質、全等三角形的判定與性質、二次函數的最值、勾股定理等知識的綜合應用.解題時得到S?BCC1B1=2S?BCDA是解決第(2)小題的關鍵.解題時注意:確定一個二次函數的最值,首先看自變量的取值范圍,當自變量取全體實數時,其最值為拋物線頂點坐標的縱坐標.


 數學奧賽暑假天天練南京大學出版社系列答案
數學奧賽暑假天天練南京大學出版社系列答案 南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案
南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案科目:初中數學 來源: 題型:填空題
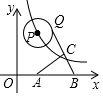 如圖,動點P在函數y=$\frac{16}{x}$(x>0)的圖象上移動,⊙P半徑為2,A(3,0),B(6,0),點Q是⊙P上的動點,點C是QB的中點,則AC的最小值是2$\sqrt{2}$-1.
如圖,動點P在函數y=$\frac{16}{x}$(x>0)的圖象上移動,⊙P半徑為2,A(3,0),B(6,0),點Q是⊙P上的動點,點C是QB的中點,則AC的最小值是2$\sqrt{2}$-1.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
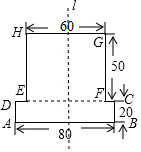 如圖是由兩個長方形組成的工件平面圖(單位:mm),直線l是它的對稱軸,若HG=60,AB=80,GF=50,CB=20,則能完全覆蓋這個平面圖形的圓面的最小半徑是50mm.
如圖是由兩個長方形組成的工件平面圖(單位:mm),直線l是它的對稱軸,若HG=60,AB=80,GF=50,CB=20,則能完全覆蓋這個平面圖形的圓面的最小半徑是50mm.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 購買蘋果數 | 不超過30kg | 30kg以上 且不超過50kg | 50kg以上 |
| 每千克價格 | 4元 | 3.5元 | 3元 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
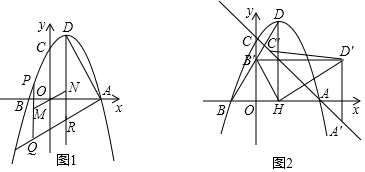
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
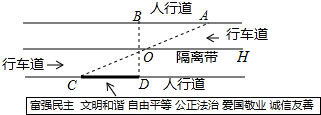
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com