
已知拋物線y=ax2+bx+c經過A(﹣1,0)、B(2,0)、C(0,2)三點.
(1)求這條拋物線的解析式;
(2)如圖一,點P是第一象限內此拋物線上的一個動點,當點P運動到什么位置時,四邊形ABPC的面積最大?求出此時點P的坐標;
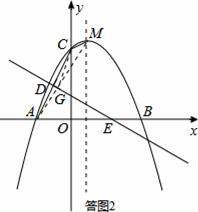
(3)如圖二,設線段AC的垂直平分線交x軸于點E,垂足為D,M為拋物線的頂點,那么在直線DE上是否存在一點G,使△CMG的周長最小?若存在,請求出點G的坐標;若不存在,請說明理由.


【考點】二次函數綜合題.
【專題】代數幾何綜合題.
【分析】方法一:
(1)利用待定系數法即可求得;
(2)如答圖1,四邊形ABPC由△ABC與△PBC組成,△ABC面積固定,則只需要使得△PBC面積最大即可.求出△PBC面積的表達式,然后利用二次函數性質求出最值;
(3)如答圖2,DE為線段AC的垂直平分線,則點A、C關于直線DE對稱.連接AM,與DE交于點G,此時△CMG的周長=CM+CG+MG=CM+AM最小,故點G為所求.分別求出直線DE、AM的解析式,聯立后求出點G的坐標.
方法二:
(1)略.
(2)由于△ABC面積為定值,因此只需△BCP面積最大時,四邊形ABPC的面積最大,利用水平底與鉛垂高乘積的一半可求出P點坐標.
(3)因為點A,C關于直線DE對稱,因此直線AM與直線DE的交點即為點G.聯立AM與DE的直線方程,可求出G點坐標.
【解答】方法一:
解:(1)∵拋物線y=ax2+bx+c經過A(﹣1,0)、B(2,0)、C(0,2)三點.
∴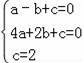
 ,解得
,解得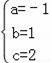
 ,
,
∴這條拋物線的解析式為:y=﹣x2+x+2.
(2)設直線BC的解析式為:y=kx+b,將B(2,0)、C(0,2)代入得:

 ,解得
,解得
 ,
,
∴直線BC的解析式為:y=﹣x+2.
如答圖1,連接BC.
四邊形ABPC由△ABC與△PBC組成,△ABC面積固定,則只需要使得△PBC面積最大即可.
設P(x,﹣x2+x+2),
過點P作PF∥y軸,交BC于點F,則F(x,﹣x+2).
∴PF=(﹣x2+x+2)﹣(﹣x+2)=﹣x2+2x.
S△PBC=S△PFC+S△PFB=
 PF(xF﹣xC)+
PF(xF﹣xC)+
 PF(xB﹣xF)=
PF(xB﹣xF)=
 PF(xB﹣xC)=PF
PF(xB﹣xC)=PF
∴S△PBC=﹣x2+2x=﹣(x﹣1)2+1
∴當x=1時,△PBC面積最大,即四邊形ABPC面積最大.此時P(1,2).
∴當點P坐標為(1,2)時,四邊形ABPC的面積最大.
(3)存在.
∵∠CAO+∠ACO=90°,∠CAO+∠AED=90°,
∴∠ACO=∠AED,又∵∠CAO=∠CAO,
∴△AOC∽△ADE,
∴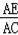
 =
=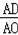
 ,即
,即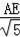
 =
=
 ,解得AE=
,解得AE=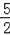
 ,
,
∴E(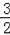
 ,0).
,0).
∵DE為線段AC的垂直平分線,
∴點D為AC的中點,∴D(﹣
 ,1).
,1).
可求得直線DE的解析式為:y=﹣
 x+
x+
 ①.
①.
∵y=﹣x2+x+2=﹣(x﹣
 )2+
)2+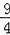
 ,∴M(
,∴M(
 ,
,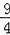
 ).
).
又A(﹣1,0),則可求得直線AM的解析式為:y=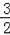
 x+
x+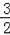
 ②.
②.
∵DE為線段AC的垂直平分線,
∴點A、C關于直線DE對稱.
如答圖2,連接AM,與DE交于點G,
此時△CMG的周長=CM+CG+MG=CM+AM最小,故點G為所求.
聯立①②式,可求得交點G的坐標為(﹣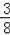
 ,
,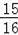
 ).
).
∴在直線DE上存在一點G,使△CMG的周長最小,點G的坐標為(﹣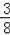
 ,
,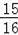
 ).
).
方法二:
(1)略.
(2)連接BC,過點P作x軸垂線,交BC′于F,
當△BCP面積最大時,四邊形ABPC的面積最大.
∵B(2,0)、C(0,2),
∴lBC:y=﹣x+2,
設P(t,﹣t2+t+2),
∴F(t,﹣t+2),
S△BCP=
 (PY﹣FY)(BX﹣CX)=
(PY﹣FY)(BX﹣CX)=
 (﹣t2+t+2+t﹣2)×2=﹣t2+2t,
(﹣t2+t+2+t﹣2)×2=﹣t2+2t,
∴當t=1時,S△BCP有最大值,即四邊形ABPC的面積最大.
∴P(1,2).
(3)∵DE為線段AC的垂直平分線,
∴點A是點C關于直線DE對稱,
∴GC=GA,
∴△CMG的周長最小時,M,G,A三點共線.
∵拋物線y=﹣x2+x+2,
∴M(
 ,
,
 ),A(﹣1,0),
),A(﹣1,0),
∴lMA:y=
 x+
x+
 ,
,
∵A(﹣1,0),C(0,2),
∴KAC=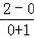
 =2,
=2,
∵AC⊥DE,∴KAC×KDE=﹣1,KDE=﹣
 ,
,
∵點D為AC的中點,
∴Dx=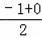
 =﹣
=﹣
 ,DY=
,DY=
 =1,
=1,
∴D(﹣
 ,1),
,1),
∴lDE:y=﹣
 x+
x+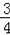
 ,
,
∴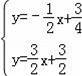
 ⇒
⇒
 ,
,
∴G(﹣
 ,
,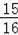
 ).
).


【點評】本題是二次函數綜合題,難度適中,綜合考查了二次函數的圖象與性質、待定系數法求解析式、相似三角形、軸對稱﹣最短路線、圖形面積計算、最值等知識點.


科目:初中數學 來源: 題型:
如圖,在平行四邊形ABCD中,E為CD上一點,連接AE、BE、BD,且AE、BD交于點F,S△DEF:S△ABF=4:25,則DE:EC=( )


A.2:3 B.2:5 C.3:5 D.3:2
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖所示的正方形網格中, 的頂點均在格點上,請在所給直角坐標系中按要求畫圖
的頂點均在格點上,請在所給直角坐標系中按要求畫圖
(1)將 向右平移1個單位長度,再向上平移4個單位長度,請畫出平移后的
向右平移1個單位長度,再向上平移4個單位長度,請畫出平移后的
(2)畫出 關于坐標原點
關于坐標原點 成中心對稱的
成中心對稱的 ;
;

查看答案和解析>>
科目:初中數學 來源: 題型:
函數y=x2+bx+c與y=x的圖象如圖所示,有以下結論:
①b2﹣4c>0;②b+c+1=0;③3b+c+6=0;④當1<x<3時,x2+(b﹣1)x+c<0.
其中正確的個數為( )


A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,已知矩形紙片的一條邊經過直角三角形紙片的直角頂點, 若矩形紙片的一組對邊與直角三角形的兩條直角邊相交成∠1、∠2,則∠2-∠
若矩形紙片的一組對邊與直角三角形的兩條直角邊相交成∠1、∠2,則∠2-∠ 1=________
1=________

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com